Perceptrons

Introduction

A perceptron is software code that models the behavior of a single biological neuron. Perceptrons were one of the earliest forms of machine learning and can be thought of as the predecessors to neural networks. The types of neural networks described in this book are also known as multilayer perceptrons. Understanding exactly what perceptrons are and how they work is almost universal for anyone who works with machine learning. Additionally, although the types of problems that can be solved using perceptrons are quite limited, an understanding of perceptrons is very helpful when learning about neural networks, which are essentially collections of perceptrons.

The best way to get a feel for where this chapter is headed is to take a look at the screenshot of a demo program shown in Figure 2-a. The image shows a console application which implements a perceptron classifier. The goal of the classifier is to predict a person's political inclination, liberal or conservative, based on his or her age and income. The demo begins by setting up eight dummy training data items:

1.5  2.0  ->  -1
2.0  3.5  ->  -1
3.0  5.0  ->  -1
3.5  2.5  ->  -1
4.5  5.0  ->   1
5.0  7.0  ->   1
5.5  8.0  ->   1
6.0  6.0  ->   1

The first data item can be interpreted to mean that a person whose age is 1.5 and whose income is 2.0 is known to be a liberal (-1). Here, age has been normalized in some way, for example by dividing actual age in years by 10 and then subtracting 0.5, so 1.5 corresponds to a person who is 20 years old. Similarly, the person represented by the first data item has had his or her income normalized in some way. The purpose of normalizing each x-data feature is to make the magnitudes of all the features relatively the same. In this case, all are between 1.0 and 10.0. Experience has shown that normalizing input data often improves the accuracy of the resulting perceptron classifier. Notice that the dummy data items have been constructed so that persons with low age and low income values are liberal, and those with high age and high income are conservative.

The first person’s political inclination is liberal, which has been encoded as -1. Conservative inclination is encoded as +1 in the training data. An alternative is to encode liberal and conservative as 0 and 1 respectively. Data normalization and encoding is an important topic in machine learning and is explained in Chapter 1. Because the variable to predict, political inclination, can have two possible values, liberal or conservative, the demo problem is called a binary classification problem.

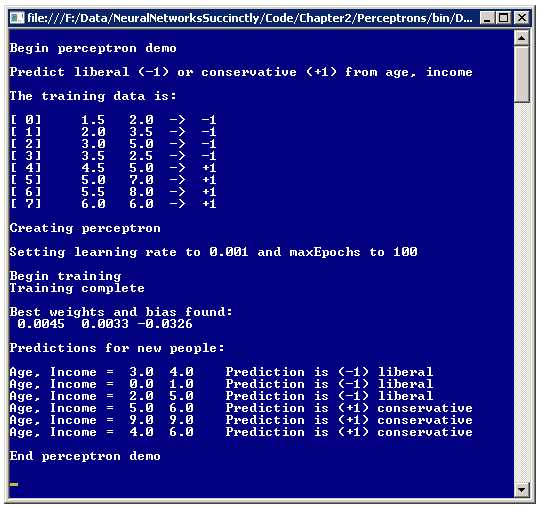
Figure 2-a: Perceptron Demo Program

After setting up the eight dummy training data items, the demo creates a perceptron with a learning rate parameter that has a value of 0.001 and a maxEpochs parameter that has a value of 100. The learning rate controls how fast the perceptron will learn. The maxEpochs parameter controls how long the perceptron will learn. Next, behind the scenes, the perceptron uses the training data to learn how to classify. When finished, the result is a pair of weights with values 0.0045 and 0.0033, and a bias value of -0.0326. These weights and bias values essentially define the perceptron model.

After training, the perceptron is presented with six new data items where the political inclination is not known. The perceptron classifies each new person as either liberal or conservative. Notice that those people with low age and income were classified as liberal, and those with high age and income were classified as conservative. For example, the second unknown data item with age = 0.0 and income = 1.0 was classified as -1, which represents liberal.

Overall Demo Program Structure

The overall structure of the demo program is presented in Listing 2-a. To create the program, I launched Visual Studio and selected the console application project template. The program has no significant .NET Framework version dependencies so any version of Visual Studio should work. I named the project Perceptrons. After the Visual Studio template code loaded into the editor, I removed all using statements except for the one that references the top-level System namespace. In the Solution Explorer window, I renamed the Program.cs file to the more descriptive PerceptronProgram.cs, and Visual Studio automatically renamed the Program class for me.

Listing 2-a: Overall Program Structure

The program class houses the Main method and two utility methods, ShowData and ShowVector. All the program logic is contained in a program-defined Perceptron class. Although it is possible to implement a perceptron using only static methods, using an object-oriented approach leads to much cleaner code in my opinion. The demo program has normal error-checking code removed in order to keep the main ideas as clear as possible.

The Input-Process-Output Mechanism

The perceptron input-process-output mechanism is illustrated in the diagram in Figure 2-b. The diagram corresponds to the first prediction in Figure 2-a where the inputs are age = x₀ = 3.0 and income = x₁ = 4.0, and the weights and bias values determined by the training process are w₀ = 0.0065, w₁ = 0.0123, and b= -0.0906 respectively. The first step in computing a perceptron's output is to sum the product of each input and the input's associated weight:

sum = (3.0)(0.0065) + (4.0)(0.0123) = 0.0687

The next step is to add the bias value to the sum:

sum = 0.0687 + (-0.0906) = -0.0219

The final step is to apply what is called an activation function to the sum. Activation functions are sometimes called transfer functions. There are several different types of activation functions. The demo program's perceptron uses the simplest type which is a step function where the output is +1 if the computed sum is greater than or equal to 0.0, or -1 if the computed sum is less than 0.0. Because the sum is -0.0219, the activation function gives -1 as the perceptron output, which corresponds to a class label of "liberal".

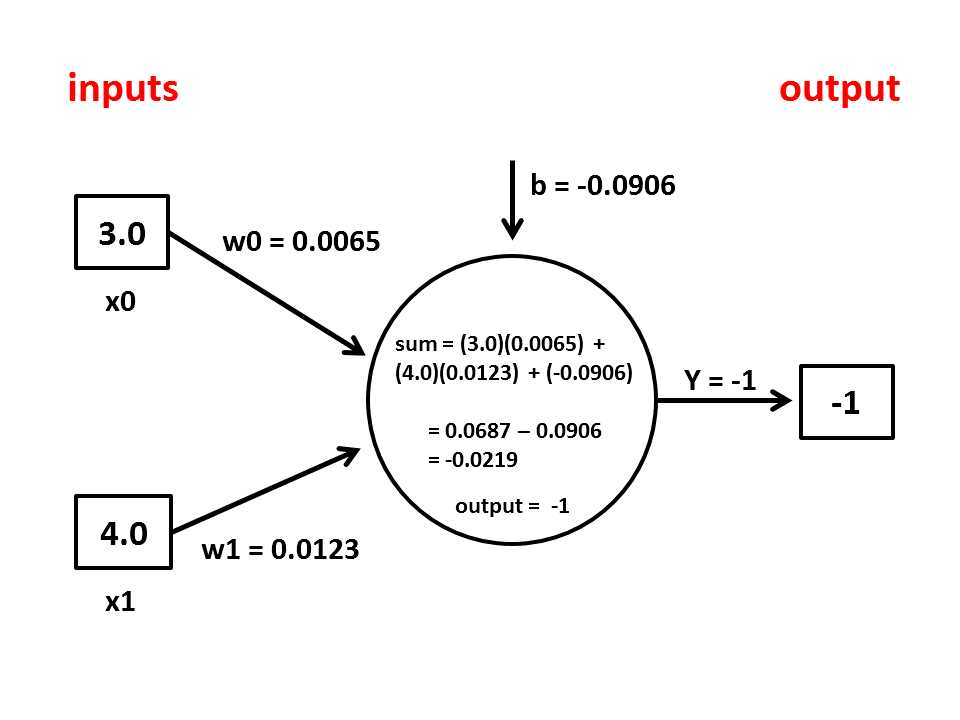
Figure 2-b: Perceptron Input-Output Mechanism

The input-process-output mechanism loosely models a single biological neuron. Each input value represents either a sensory input or the output value from some other neuron. The step function activation mimics the behavior of certain biological neurons which either fire or do not, depending on whether the weighted sum of input values exceeds some threshold.

One factor that can cause great confusion for beginners is the interpretation of the bias value. A perceptron bias value is just a constant that is added to the processing sum before the activation function is applied. Instead of treating the bias as a separate constant, many references treat the bias as a special type of weight with an associated dummy input value of 1.0. For example, in Figure 2-b, imagine that there is a third input node with value 1.0 and that the bias value b is now labeled as w₂. The sum would be computed as:

sum = (3.0)(0.0065) + (4.0)(0.0123) + (1.0)(-0.0906) = -0.0219

which is exactly the same result as before. Treating the bias as a special weight associated with a dummy input value of 1.0 is a common approach in research literature because the technique simplifies several mathematical proofs. However, treating the bias as a special weight has two drawbacks. First, the idea is somewhat unappealing intellectually. In my opinion, a constant bias term is clearly, conceptually distinct from a weight associated with an input because the bias models a real neuron's firing threshold value. Second, treating a bias as a special weight introduces the minor possibility of a coding error because the dummy input value can be either the first input (x₀ in the demo) or the last input (x₂).

The Perceptron Class Definition

The structure of the Perceptron class is presented in Listing 2-b. The integer field numInput holds the number of x-data features. For example, in the demo program, numInput would be set to 2 because there are two predictor variables, age and income.

The type double array field named "inputs" holds the values of the x-data. The double array field named "weights" holds the values of the weights associated with each input value both during and after training. The double field named "bias" is the value added during the computation of the perceptron output. The integer field named "output" holds the computed output of the perceptron. Field "rnd" is a .NET Random object which is used by the Perceptron constructor and during the training process.

Listing 2-b: The Perceptron Class

The Perceptron class exposes three public methods: a class constructor, method Train, and method ComputeOutput. The class has four private helper methods: method InitializeWeights is called by the class constructor, method Activation is called by ComputeOutput, and methods Shuffle and Update are called by Train.

The Perceptron class constructor is defined:

public Perceptron(int numInput)
{
  this.numInput = numInput;
  this.inputs = new double[numInput];
  this.weights = new double[numInput];
  this.rnd = new Random(0);
  InitializeWeights();
}

The constructor accepts the number of x-data features as input parameter numInput. That value is used to instantiate the class inputs array and weights array. The constructor instantiates the rnd Random object using a hard-coded value of 0 for the seed. An alternative is to pass the seed value as an input parameter to the constructor. In general, instantiating a Random object with a fixed seed value is preferable to calling the constructor overload with no parameter because a fixed seed allows you to reproduce training runs.

The constructor code finishes by calling private helper method InitializeWeights. Method InitializeWeights assigns a different, small random value between -0.01 and +0.01 to each perceptron weight and the bias. The method is defined as:

private void InitializeWeights()
{
  double lo = -0.01;
  double hi = 0.01;
  for (int i = 0; i < weights.Length; ++i)
    weights[i] = (hi - lo) * rnd.NextDouble() + lo;
  bias = (hi - lo) * rnd.NextDouble() + lo;
}

The random interval of [-0.01, +0.01] is hard-coded. An alternative is to pass one or both interval end points to InitializeWeights as parameters. This approach would require you to either make the scope of InitializeWeights public so that the method can be called separately from the constructor, or to add the interval end points as parameters to the constructor so that they can be passed to InitializeWeights.

The ComputeOutput Method

Public method ComputeOutput accepts an array of input values and uses the perceptron's weights and bias values to generate the perceptron output. Method ComputeOutput is presented in Listing 2-c.

Listing 2-c: ComputeOutput Method

After a check to verify that the size of the input array parameter is correct, the method copies the values in the array parameter into the class inputs array. Because method ComputeOutput will typically be called several hundred or thousand times during the training process, an alternative design approach is to eliminate the class inputs array field and compute output directly from the x-values array parameter. This alternative approach is slightly more efficient but a bit less clear than using an explicit inputs array.

Method ComputeOutput computes a sum of the products of each input and its associated weight, adds the bias value, and then applies the step activation function. An alternative design is to delete the simple activation method definition and place the activation code logic directly into method ComputeOutput. However, a separate activation method has the advantage of being a more modular design and emphasizing the separate nature of the activation function.

The step activation function is defined as:

private static int Activation(double v)
{
  if (v >= 0.0)
    return +1;
  else
    return -1;
}

Recall that the demo problem encodes the two y-values to predict as -1 for liberal and +1 for conservative. If you use a 0-1 encoding scheme you would have to modify method Activation to return those two values.

Training the Perceptron

Training a perceptron is the process of iteratively adjusting the weights and bias values so that the computed outputs for a given set of training data x-values closely match the known outputs. Expressed in high-level pseudo-code, the training process is:

loop
  for each training item
    compute output using x-values
    compare computed output to known output
    if computed is too large
      make weights and bias values smaller
    else if computed is too small
      make weights and bias values larger
    end if
  end for
end loop

Although training is fairly simple conceptually, the implementation details are a bit tricky. Method Train is presented in Listing 2-d. Method Train accepts as input parameters a matrix of training data, a learning rate alpha, and a loop limit maxEpochs. Experience has shown that in many situations it is preferable to iterate through the training data items using a random order each time through the main processing loop rather than using a fixed order. To accomplish this, method Train uses an array named sequence. Each value in array sequence represents an index into the row of the training data. For example, the demo program has eight training items. If array sequence held values { 7, 1, 0, 6, 4, 3, 5, 2 }, then row 7 of the training data would be processed first, row 1 would be processed second, and so on.

Helper method Shuffle is defined as:

private void Shuffle(int[] sequence)
{
  for (int i = 0; i < sequence.Length; ++i)
  {
    int r = rnd.Next(i, sequence.Length);
    int tmp = sequence[r];
    sequence[r] = sequence[i];
    sequence[i] = tmp;
  }
}

Method Shuffle uses the Fisher-Yates algorithm to scramble the values in its array parameter. The key to the training algorithm is the helper method Update, presented in Listing 2-e. Method Update accepts a computed output value, the desired output value from the training data, and a learning rate alpha. Recall that computed and desired output values are either -1 (for liberal) or +1 (for conservative).

Listing 2-d: The Train Method

Method Update calculates the difference between the computed output and the desired output and stores the difference into the variable delta. Delta will be positive if the computed output is too large, or negative if computed output is too small. For a perceptron with -1 and +1 outputs, delta will always be either -2 (if computed = -1 and desired = +1), or +2 (if computed = +1 and desired = -1), or 0 (if computed equals desired).

For each weight[i], if the computed output is too large, the weight is reduced by amount (alpha * delta * input[i]). If input[i] is positive, the product term will also be positive because alpha and delta are also positive, and so the product term is subtracted from weight[i]. If input[i] is negative, the product term will be negative, and so to reduce weight[i] the product term must be added.

Notice that the size of the change in a weight is proportional to both the magnitude of delta and the magnitude of the weight's associated input value. So a larger delta produces a larger change in weight, and a larger associated input also produces a larger weight change.

The learning rate alpha scales the magnitude of a weight change. Larger values of alpha generate larger changes in weight which leads to faster learning, but at a risk of overshooting a good weight value. Smaller values of alpha avoid overshooting but make training slower.

Listing 2-e: The Update Method

The weight adjustment logic leads to four control branches in method Update, depending on whether delta is positive or negative, and whether input[i] is positive or negative. Inputs are assumed to not be zero so you might want to check for this. In pseudo-code:

if computed > desired and input > 0 then
  weight = weight - (alpha * delta * input)
else if computed > desired and input < 0 then
  weight = weight + (alpha * delta * input)
else if computed < desired and input > 0 then
  weight = weight - (alpha * delta * input)
else if  computed < desired and input < 0 then
  weight = weight + (alpha * delta * input)
end if

If you examine the logic closely you can see that the first and third branches, and the second and fourth branches can be combined so the previous pseudo-code is equivalent to:

if input > 0 then
  weight = weight - (alpha * delta * input)
else
  weight = weight + (alpha * delta * input)
end if

And, in situations where the input data has been normalized so that all values are non-negative, the update logic can be condensed even further, like so:

weight = weight - (alpha * delta * input) /* assumes input > 0 */

In my opinion, the four-branch logic is the most clear but least efficient, and the single-branch logic is most efficient but least clear. In most cases, the performance impact of the four-branch logic will not be significant.

Updating the bias value does not depend on the value of an associated input, so the logic is:

if computed > desired then
  bias = bias - (alpha * delta)
else
  bias = bias - (alpha * delta)
end if

Therefore, the code logic can be simplified to just:

bias = bias – (alpha * delta)

Notice that all the update logic depends on the way in which delta is computed. The demo arbitrarily computes delta as (computed - desired). If you choose to compute delta as (desired - computed) then you would have to adjust the update code logic appropriately.

The learning rate alpha and the loop count limit maxEpochs are sometimes called free parameters. These are values that must be supplied by the user. The term free parameters is also used to refer to the perceptron's weights and bias because these values are free to vary during training. In general, the best choice of values for perceptron and neural network free parameters such as the learning rate must be found by trial and error experimentation. This unfortunate characteristic is common to many forms of machine learning.

Using the Perceptron Class

The key statements in the Main method of the demo program which create and train the perceptron are:

int numInput = 2;
Perceptron p = new Perceptron(numInput);
double alpha = 0.001;
int maxEpochs = 100;
double[] weights = p.Train(trainData, alpha, maxEpochs);

The interface is very simple; first a perceptron is created and then it is trained. The final weights and bias values found during training are returned by the Train method. An alternative design is to implement a property GetWeights and call along the lines of:

double alpha = 0.001;
int maxEpochs = 100;
p.Train(trainData, alpha, maxEpochs);
double[] weights = p.GetWeights();

The code for the Main method of the demo program is presented in Listing 2-f. The training data is hard-coded:

double[][] trainData = new double[8][];

trainData[0] = new double[] { 1.5, 2.0, -1 };
// etc.

Listing 2-f: The Main Method

In many situations, training data is stored externally, for example in a text file or SQL database. In these situations you will have to write a utility method to load the data into memory along the lines of:

string dataLocation = "C:\\Data\\AgeIncome.txt";
double[][] trainData = LoadData(dataLocation);

The perceptron demo program has two helper methods, ShowData and ShowVector, to display the contents of the training data matrix and the contents of an array of type double. The code for these two helper methods is presented in Listing 2-g.

Listing 2-g: Helper Methods ShowData and ShowVector

Making Predictions

In the Main method, after the perceptron has been instantiated and trained to classify a person's political inclination based on his or her age and income, the perceptron is presented with six new data items where the political inclination is not known:

double[][] newData = new double[6][];

newData[0] = new double[] { 3.0, 4.0 }; // Output should be -1.

newData[1] = new double[] { 0.0, 1.0 }; // Should be -1.

newData[2] = new double[] { 2.0, 5.0 }; // Should be -1.

newData[3] = new double[] { 5.0, 6.0 }; // Should be 1.

newData[4] = new double[] { 9.0, 9.0 }; // Should be 1.

newData[5] = new double[] { 4.0, 6.0 }; // Should be 1.

The key code to predict political inclination for newData item [i] is:

int c = p.ComputeOutput(newData[i]);

Console.Write("Prediction is ");

if (c == -1)

  Console.WriteLine("(-1) liberal");

else if (c == 1)

  Console.WriteLine("(+1) conservative");

After training, the perceptron holds weights and bias values that generate computed y-value outputs that closely match the known y-value outputs of the training data. These weights and bias values are used by method ComputeOutput to generate a -1 or +1 output.

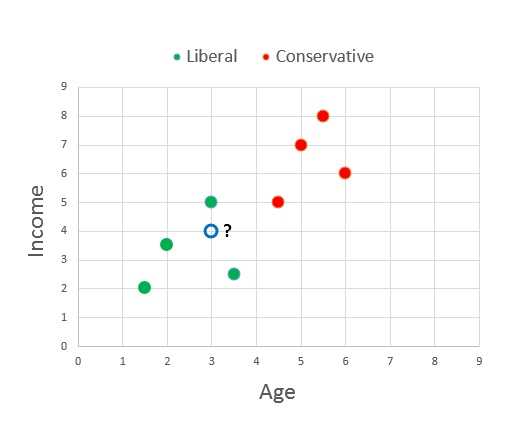
Figure 2-c: Predicting Liberal or Conservative

The graph in Figure 2-c illustrates how perceptron prediction works. The green and red dots are the training data. The open blue dot with the question mark is newData[0] where age is 3.0 and income is 4.0 (normalized). From the graph, it's pretty obvious that the new person is more likely liberal (green) than conservative (red).

Training a perceptron essentially finds a straight line so that all the training data items in one class (for example, liberal in the demo) are on one side of the line and all the items in the other class (conservative) are on the other side of the line. This characteristic of perceptrons is called linear separability. Notice that there are many possible separating lines.

Limitations of Perceptrons

Soon after the first perceptrons were studied in the 1950s, it became clear that perceptrons have several weaknesses that limit their usefulness to only simple classification problems.

Because perceptrons essentially find a separating line between training data y-value classes, perceptrons can only make good predictions in situations where this is possible.

Put slightly differently, suppose that in Figure 2-c the training data were positioned in such a way that there was a clear distinction between liberal and conservative, but the dividing space between classes was a curved, rather than straight, line. A simple perceptron would be unable to handle such a situation. In general, with real-life data it's not possible to know in advance whether the training data is linearly separable or not.

Another weakness of the perceptron implementation presented here is related to the training process. In the demo, the training loop executes a fixed number of times specified by the maxEpochs variable. What is really needed is a measure of error so that training can be stopped when the overall error drops below some threshold value. As it turns out, the notion of a training error term is closely related to the activation function. The demo perceptron uses a simple step function which does not lend itself well to an error function. The limitations of the simple perceptron model gave rise to neural networks in the 1980s.

Neural networks have two main enhancements over perceptrons. First, a neural network has many processing nodes, instead of just one, which are organized into two layers. This is why neural networks are sometimes called multilayer perceptrons. Second, neural networks typically use activation functions which are more sophisticated than the step function typically used by perceptrons. Both enhancements increase the processing power of neural networks relative to perceptrons.

In the late 1980s, neural network research proved that, loosely speaking, a fully connected feed-forward neural network that uses a sophisticated activation function can approximate any continuous mathematical function. This is called the universal approximation theorem, or sometimes the Cybenko theorem. What this means is that neural networks can accurately classify data if it is possible to separate the y-data using any smooth, curved line or surface.

For example, take another look at the graph of political inclination based on age and income in Figure 2-c. A perceptron can only classify correctly when it is possible to draw a straight line on the graph so that all the conservative data points are on one side of the line and all the liberal data points are on the other side. But a neural network can classify correctly when it is possible to draw any smooth, curved line to separate the two classes.

Complete Demo Program Source Code