Feed-Forward

---

Introduction

A neural network is essentially a mathematical function that accepts one or more numeric inputs and produces one or more numeric outputs. The basic neural network input-process-output computation is called the feed-forward mechanism. Understanding the feed-forward mechanism is essential to understanding how to create neural networks that can make predictions.

The best way to get a feel for where this chapter is headed is to take a look at the screenshot of a demo program shown in Figure 3-a and the associated diagram in Figure 3-b. Both figures illustrate the same dummy neural network with three inputs and two outputs. The dummy input values are 1.0, 2.0, and 3.0, and the output values generated are 0.4920 and 0.5080. The demo neural network has an internal layer of four hidden nodes. The neural network has 26 constants called weights and biases that are used during the computation of the output values.

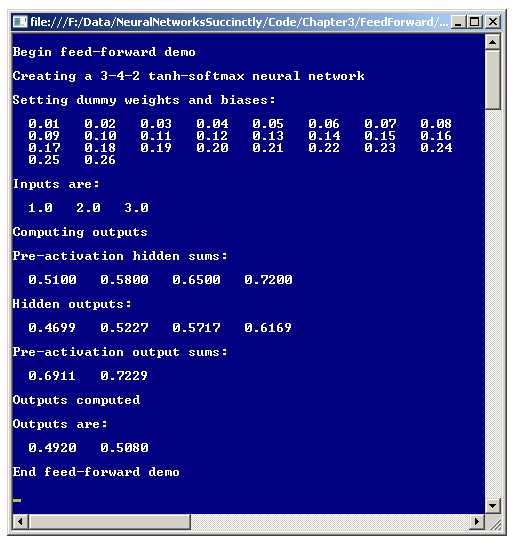
Figure 3-a: Feed-Forward Mechanism Demo

The demo program in Figure 3-a displays some intermediate values during the computation of the outputs. These intermediate values, the pre-activation hidden sums, hidden outputs, and pre-activation output sums normally would not be shown and are there just to help you understand the feed-forward mechanism.

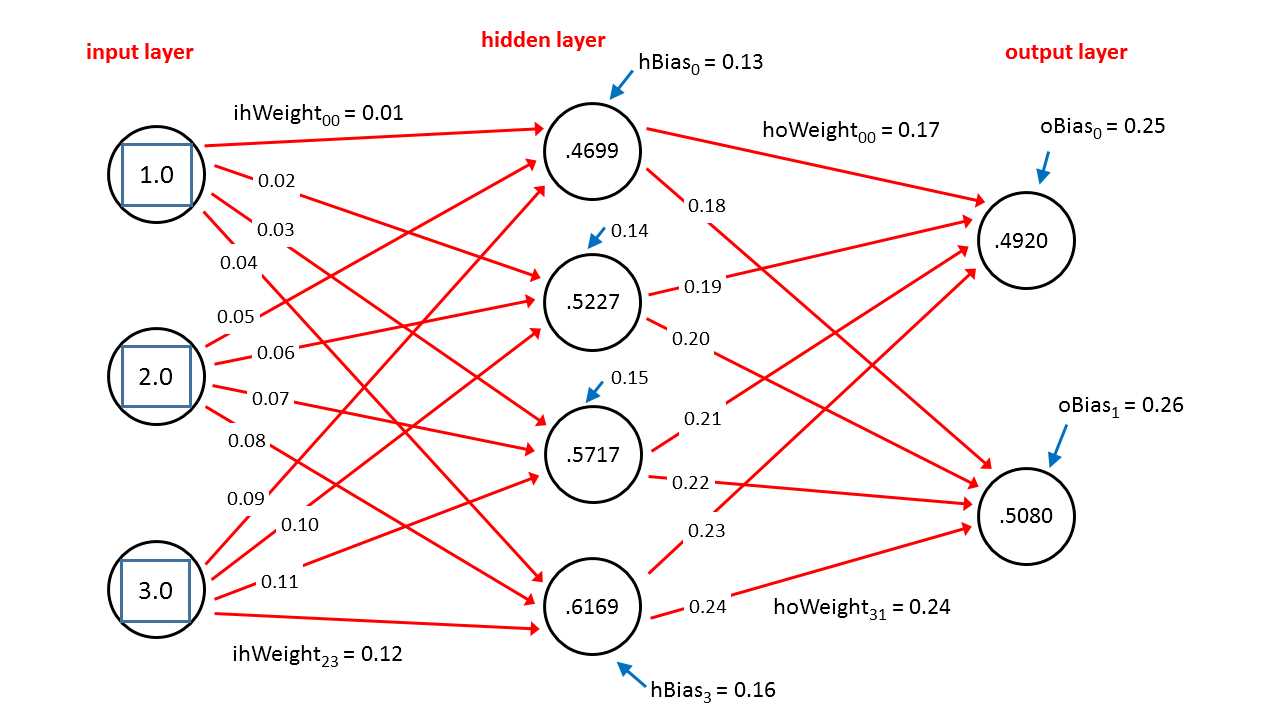
Figure 3-b: Neural Network Architecture

Understanding Feed-Forward

A neural network computes its outputs in several steps and the feed-forward mechanism is best explained using a concrete example. In Figure 3-b, there are three dummy inputs with values 1.0, 2.0, and 3.0. In the figure, objects are zero-based indexed, from top to bottom, so the top-most input with value 1.0 is inputs[0] and the bottom-most input with value 3.0 is inputs[2].

Each red line connecting one node to another represents a weight constant. The top-most weight with value 0.01 is labeled ihWeight[0][0], which means the weight from input node 0 to hidden node 0. Similarly, the weight in the lower right corner of Figure 3-b, with value 0.24, is labeled hoWeight[3][1] which means the weight from hidden node 3 to output node 1.

Each of the hidden and output layer nodes has an arrow pointing to it. These are called the bias values. The bias value at the top of the figure with value 0.13 is labeled hBias[0] which means the bias value for hidden node 0.

The first step in the feed-forward mechanism is to compute the values shown in the hidden layer nodes. The value of hidden node 0 is 0.4699 and is computed as follows. First, the product of each input value and its associated weight are summed:

hSums[0] = (1.0)(0.01) + (2.0)(0.05) + (3.0)(0.09) = 0.01 + 0.10 + 0.27 = 0.38

Next, the associated bias value is added:

hSums[0] = 0.38 + 0.13 = 0.51

In Figure 3-a, you can see this displayed as the first pre-activation sum. Next, a so-called activation function is applied to the sum. Activation functions will be explained in detail later, but for now it's enough to say that the activation function is the hyperbolic tangent function, which is usually abbreviated tanh.

hOutputs[0] = tanh(0.51) = 0.4699

You can see the 0.4699 displayed as the first hidden output in Figure 3-a, and also as the value inside the top-most hidden node in Figure 3-b. The other three hidden nodes are computed in the same way. Here, the steps are combined to save space:

hOutputs[1] = tanh( (1.0)(0.02) + (2.0)(0.06) + (3.0)(0.10) + 0.14 ) = tanh(0.58) = 0.5227
hOutputs[2] = tanh( (1.0)(0.03) + (2.0)(0.07) + (3.0)(0.11) + 0.15 ) = tanh(0.65) = 0.5717
hOutputs[3] = tanh( (1.0)(0.04) + (2.0)(0.08) + (3.0)(0.12) + 0.16 ) = tanh(0.72) = 0.6169

After all hidden node output values have been computed, these values are used as inputs to the output layer. The output node values are computed slightly differently from the hidden nodes. The preliminary output sums, before activation, for output nodes 0 and 1 are computed the same way as the preliminary hidden node sums, by summing products of inputs and weights and then adding a bias value:

oSums[0] = (0.4699)(0.17) + (0.5227)(0.19) + (0.5717)(0.21) + (0.6169)(0.23) + 0.25 = 0.6911
oSums[1] = (0.4699)(0.18) + (0.5227)(0.20) + (0.5717)(0.22) + (0.6169)(0.24) + 0.26 = 0.7229

The activation function for the output layer is called the softmax function. This will be explained later, but for now the softmax of each preliminary sum is best explained by example:

output[0] = exp(0.6911) /  (exp(0.6911) + exp(0.7229)) = 1.9959 / (1.9959 + 2.0604) = 0.4920
output[1] = exp(0.7229) /  (exp(0.6911) + exp(0.7229)) = 2.0604 / (1.9959 + 2.0604) = 0.5080

If you look at both Figures 3-a and 3-b, you will see these are the final output values computed by the demo neural network. Here, the exp function of some value x is the math constant e = 2.71828. . . raised to the xth power. Notice the two output values sum to 1.0, which is not a coincidence and is the point of using the softmax function.

To summarize, a neural network is essentially a mathematical function whose outputs are determined by the input values, a number of hidden nodes, a set of weights and bias values, and two activation functions. The architecture presented here is called a fully-connected network, because the nodes in a given layer are connected to all the nodes in the next layer. It is possible to design neural networks that are not fully connected.

Bias Values as Special Weights

When working with neural networks, you must pay careful attention to how the bias values are handled. In the previous section, bias values are treated as distinct constants. However, the majority of neural network research treats biases as special weights associated with a dummy input value of 1.0.

For example, in Figure 3-b, the bias value for hidden node 0 is 0.13. The pre-activation sum for hidden node 0, if the bias is treated as a true bias, is computed as:

hSum[0] = (1.0)(0.01) + (2.0)(0.05) + (3.0)(0.09) + 0.13 = 0.51

If you imagine a dummy input node with the value 1.0 next to hidden node 0, and consider the bias as a special weight, the pre-activation sum would be computed as:

hSum[0] = (1.0)(0.01) + (2.0)(0.05) + (3.0)(0.09) + (1.0)(0.13) = 0.51

In other words, the result is the same. The point of treating a bias as a special weight is that doing so simplifies many of the mathematical proofs and derivations in research. But from a developer's point of view, treating a bias as a special weight is conceptually awkward and, in my opinion, more error-prone than treating all biases as true biases.

Overall Demo Program Structure

The overall structure of the demo program is presented in Listing 3-a. After the Visual Studio template code loaded into the editor, I removed all using statements except for the one that references the top-level System namespace. In the Solution Explorer window, I renamed the Program.cs file to the more descriptive FeedForwardProgram.cs, and Visual Studio automatically renamed the Program class for me.

Listing 3-a: Overall Program Structure

The program class houses the Main method and a utility method ShowVector. All the program logic is contained in a program-defined NeuralNetwork class. Although it is possible to implement a neural network using only arrays and static methods, using an object-oriented approach leads to easier-to-understand code in my opinion. The demo program has most normal error checking removed in order to keep the main ideas as clear as possible.

The Main method begins by instantiating the demo neural network:

static void Main(string[] args)

{

  Console.WriteLine("\nBegin feed-forward demo\n");
  int numInput = 3;

  int numHidden = 4;

  int numOutput = 2;

  Console.WriteLine("Creating a 3-4-2 tanh-softmax neural network");

  NeuralNetwork nn = new NeuralNetwork(numInput, numHidden, numOutput);

Notice that the demo neural network constructor accepts parameter values for the number of input nodes, the number of hidden nodes, and the number of output nodes. This means that the two activation functions used, tanh and softmax, are hardwired into the network.

The demo program continues by setting up 26 dummy weights and bias values and then placing them into the neural network using a method SetWeights:

double[] weights = new double[] {

   0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10,

   0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.19, 0.20,

   0.21, 0.22, 0.23, 0.24, 0.25, 0.26

};

Console.WriteLine("\nSetting dummy weights and biases:");

ShowVector(weights, 8, 2, true);

nn.SetWeights(weights);

If you refer to the diagram in Figure 3-b you can see the relationship between the architecture of a neural network and the number of weights and bias values. Because there is a weight from each input node to each hidden node, there are (numInput * numHidden) input-to-hidden weights. Each hidden node has a bias value so there are numHidden hidden node biases. There is a weight from each hidden node to each output node, making (numHidden * numOutput) weights. And each output node has a bias making numOutput more biases. Putting this all together, there are a total of (numInput * numHidden) + numHidden + (numHidden * numOutput) + numOutput weights and bias values.

Next, the demo sets up and displays three arbitrary input values:

double[] xValues = new double[] { 1.0, 2.0, 3.0 };

Console.WriteLine("\nInputs are:");

ShowVector(xValues, 3, 1, true);

The demo program concludes by computing and displaying the output values:

  Console.WriteLine("\nComputing outputs");

  double[] yValues = nn.ComputeOutputs(xValues);

  Console.WriteLine("\nOutputs computed");

  Console.WriteLine("\nOutputs are:");

  ShowVector(yValues, 2, 4, true);
  Console.WriteLine("\nEnd feed-forward demo\n");

  Console.ReadLine();

} // Main

The code for utility method ShowVector is:

public static void ShowVector(double[] vector, int valsPerRow,

  int decimals, bool newLine)

{

  for (int i = 0; i < vector.Length; ++i)

  {

    if (i % valsPerRow == 0)

      Console.WriteLine("");

    Console.Write(vector[i].ToString("F" + decimals).PadLeft(decimals + 4) + " ");

  }

  if (newLine == true)

    Console.WriteLine("");

}

The ShowVector method is declared with public scope so that it can be called inside methods in the NeuralNetwork class.

Designing the Neural Network Class

There are many ways to implement a neural network in code. The design presented in Listing 3-b emphasizes simplicity over efficiency. Member fields numInput, numHidden, and numOutput store the number of input nodes, hidden nodes, and output nodes. The array member named inputs holds the numeric inputs to the neural network. Interestingly, as will be shown shortly, the inputs array can be omitted for slightly increased processing efficiency.

Matrix member ihWeights holds the weights from input nodes to hidden nodes, where the row index corresponds to the index of an input node, and the column index corresponds to the index of a hidden node. The matrix is implemented as an array of arrays. Unlike most programming languages, C# has a true multidimensional array and you may want to use that approach to store the neural network weights.

Member array hBiases holds the bias values for the hidden nodes. Many implementations you'll find will omit this array and instead treat the hidden node biases as extra input-to-hidden weights.

Member array hOutputs stores the hidden node outputs after summing the products of weights and inputs, adding the bias value, and applying an activation function during the computation of the output values. An alternative is to make this array local to the ComputeOutputs. However, because in most situations the ComputeOutputs method is called many thousands of times, a local array would have to be allocated many times. Naming array hOutputs is a bit tricky because the values also serve as inputs to the output layer.

Member matrix hoWeights holds the weights from hidden nodes to output nodes. The row index of the matrix corresponds to the index of a hidden node and the column index corresponds to the index of an output node.

Member array oBiases holds bias values for the output nodes. The member array named outputs holds the final overall computed neural network output values. As with the inputs array, you'll see that the outputs array can potentially be dropped from the design.

Listing 3-b: Designing a Neural Network Class

The neural network class in Listing 3-b has three public methods: a constructor, a method to set the values of the weights and biases, and a method that computes and returns the output values. In later chapters, as training features are added to the neural network, additional public-scope methods will be added to the class definition.

Private method MakeMatrix is a helper method called by the constructor. Private helper methods HyperTan and Softmax are called by method ComputeOutputs.

The Neural Network Constructor

The NeuralNetwork class constructor begins by copying each input parameter value to its associated member field:

public NeuralNetwork(int numInput, int numHidden, int numOutput)

{

  this.numInput = numInput;

  this.numHidden = numHidden;

  this.numOutput = numOutput;

Next, space for the inputs array is allocated:

this.inputs = new double[numInput];

Next, the constructor allocates space for the input-to-hidden weights matrix using helper method MakeMatrix:

this.ihWeights = MakeMatrix(numInput, numHidden);

An alternative is to allocate the matrix directly, but using a helper method makes sense here because the helper can be reused when allocating the hidden-to-output weights matrix. Method MakeMatrix is defined as:

private static double[][] MakeMatrix(int rows, int cols)

{

  double[][] result = new double[rows][];

  for (int i = 0; i < rows; ++i)

    result[i] = new double[cols];

  return result;

}

Depending on your background, you may be unfamiliar with working with C# array-of-arrays style matrices. The matrix syntax does not correspond closely to most normal programming idioms and can take a while to get accustomed to.

The NeuralNetwork class constructor finishes by allocating space for the remaining member matrix and four arrays:

  this.hBiases = new double[numHidden];

  this.hOutputs = new double[numHidden];

  this.hoWeights = MakeMatrix(numHidden, numOutput);

  this.oBiases = new double[numOutput];

  this.outputs = new double[numOutput];

}

Setting Neural Network Weights and Bias Values

The demo program uses a method SetWeights to populate weight matrices ihWeights and hoWeights, and bias arrays hBiases and oBiases with values. Method SetWeights is presented in Listing 3-c. Method SetWeights accepts a single array parameter which holds all the weights and bias values.

The method assumes that the values in the weights array parameter are stored in a particular order: first the input-to-hidden weights, followed by the hidden biases, followed by the hidden-to-output weights, followed by the output biases. Additionally, the values for the two weights matrices are assumed to be stored in row-major order. This means the values are ordered from left to right and top to bottom.

As usual, a concrete example is the best way to explain. The demo neural network shown in Figure 3-b was created by passing an array with values { 0.01, 0.02, 0.03, . . 0.26 } to the SetWeights method. This populates matrix ihWeights with values:

0.01  0.02  0.03  0.04
0.05  0.06  0.07  0.08
0.09  0.10  0.11  0.12

The hBiases array gets:

0.13  0.14  0.15  0.16

Matrix hoWeights gets:

0.17  0.18
0.19  0.20
0.21  0.22
0.23  0.24

And the oBiases array gets:

0.25  0.26

This assumption of a particular ordering of the values in the array parameter passed to method SetWeights is somewhat brittle. The alternative is to explicitly pass two matrices and two arrays to SetWeights, but in my opinion, the extra complexity outweighs the increased safety unless you were designing your neural network for use by others.

Listing 3-c: Setting Weights and Bias Values

Computing Outputs

Method ComputeOutputs implements the feed-forward mechanism. The method, with diagnostic WriteLine statements removed, is presented in Listing 3-d. The method definition begins by doing a simple check on the input values:

public double[] ComputeOutputs(double[] xValues)

{

  if (xValues.Length != numInput)

    throw new Exception("Bad xValues array");

In a realistic neural network scenario, you might want to consider dropping this input parameter check to improve performance. An alternative is to pass in a Boolean flag parameter named something like checkInput to indicate whether or not to perform the error check; however, in this case checking the value of the Boolean would incur as much overhead as performing the error check itself.

Listing 3-d: Computing Neural Network Output Values

Next, method ComputeOutputs creates and allocates scratch arrays to hold the pre-activation sum of products of inputs and weights plus a bias value:

double[] hSums = new double[numHidden];

double[] oSums = new double[numOutput];

Recall that in C#, when an array of type double is created, the cell values are automatically set to 0.0. As mentioned previously, in most situations, when a neural network is being trained, the feed-forward mechanism is called many thousands of times. So, at first thought, the alternative of declaring the two arrays as class-scope fields rather than repeatedly allocating the two scratch sum arrays inside method ComputeOutputs is appealing. However, this has the downside of cluttering up the class definition. Additionally, because these scratch arrays hold accumulations of sums, the array would have to be zeroed-out at the beginning of ComputeOutputs, which negates most of the advantage of not having to allocate the arrays.

Next, the input values are copied from the xValues array parameter into the member inputs array:

for (int i = 0; i < xValues.Length; ++i)

  inputs[i] = xValues[i];

A syntactic alternative is to use the C# Array.Copy method. If you review the feed-forward mechanism carefully, you'll see that the values in the member array named inputs are used but not changed. Therefore it is possible to eliminate the inputs array and just use the values in the xValues array. Because method ComputeOutputs might be called thousands or even millions of times depending upon the usage scenario, eliminating an unnecessary array copy could save significant time.

Eliminating the inputs member array has at least two disadvantages, however. First, conceptually, a neural network does have inputs and so eliminating them just doesn't feel quite right in some subjective way. Second, if you implement a class ToString method, you'd certainly want to be able to see the current values of the inputs which would not be possible if the inputs array is not in the class definition.

An alternative is to pass a Boolean flag parameter named copyInputs to the method ComputeOutputs along the lines of:

public double[] ComputeOutputs(double[] xValues, bool copyInputs)

{

  if (copyInputs == true)

  {

    for (int i = 0; i < xValues.Length; ++i)

      inputs[i] = xValues[i];

  }

  else

    inputs = xValues;

Using this approach would improve performance at the minor risk of a possible unwanted side effect; in the else-branch when parameter copyInputs is false, the inputs array is assigned a reference (essentially a pointer) to the xValues array. Any change to one of the arrays effectively changes the other array. In short, explicitly copying the xValues array values to the inputs member array is safer and clearer but has slower performance than implicitly copying using a reference.

After copying values into the inputs member array, method ComputeOutputs accumulates the sum of products of input-to-hidden weights and inputs:

for (int j = 0; j < numHidden; ++j)

  for (int i = 0; i < numInput; ++i)

    hSums[j] += inputs[i] * ihWeights[i][j];

Although short, the code is somewhat tricky because of the array indexing. In this case, index j points into the hidden sums array and also acts as the column index into the input-to-hidden weights matrix. As a general rule, based on my experience, most of the bugs in my neural network implementations are related to array and matrix indexing. Developers have different approaches to coding, but for me, drawing pictures of my arrays and matrices and indices, using paper and pencil, is the only way I can keep my indices correct.

Next, the bias values are added to the accumulated hidden node sums:

for (int i = 0; i < numHidden; ++i)

  hSums[i] += hBiases[i];

Console.WriteLine("\nPre-activation hidden sums:");

FeedForwardProgram.ShowVector(hSums, 4, 4, true);

In the demo program, the hidden sums are displayed only for informational purposes. In a realistic, non-demo scenario these sums would not be displayed. One common approach is to pass in a Boolean parameter, often named "verbose", to control whether or not to print diagnostic messages.

Next, the hyperbolic tangent activation function is applied to each sum to give the hidden node's output values:

for (int i = 0; i < numHidden; ++i)

  hOutputs[i] = HyperTan(hSums[i]);

Console.WriteLine("\nHidden outputs:");

FeedForwardProgram.ShowVector(hOutputs, 4, 4, true);

Activation functions will be discussed in detail in the following section of this chapter. For now, notice that the HyperTan function accepts a single value of type double and returns a single value of type double. Therefore, the function must be applied individually to each hidden sum.

Next, method ComputeOutputs computes the pre-activation sums for the output layer nodes:

for (int j = 0; j < numOutput; ++j)

  for (int i = 0; i < numHidden; ++i)

    oSums[j] += hOutputs[i] * hoWeights[i][j];

for (int i = 0; i < numOutput; ++i)

  oSums[i] += oBiases[i];

Console.WriteLine("\nPre-activation output sums:");

FeedForwardProgram.ShowVector(oSums, 2, 4, true);

Next, softmax activation is applied to the sums and the final results are stored into the outputs array:

double[] softOut = Softmax(oSums);

  for (int i = 0; i < outputs.Length; ++i)

    outputs[i] = softOut[i];

Notice that unlike the HyperTan method, method Softmax accepts an array of double values and returns an array of double values.

Method ComputeOutputs finishes by copying the values in the class member array named outputs to a local method return result array and then returning that array:

  double[] result = new double[numOutput];

  for (int i = 0; i < outputs.Length; ++i)

    result[i] = outputs[i];

  return result;

} // ComputeOutputs

In effect, method ComputeOutputs returns the output values of the neural network in two ways: first, stored into class member array outputs, and second, as an explicit return value. This idea is a bit subtle and is mostly for calling flexibility. Explicitly returning the neural network outputs allows you to fetch the outputs into an array with a call like:

double[] yValues = nn.ComputeOutputs(xValues);

The output values also reside in the neural network object, so if you implement a GetOutputs method you could make a call along the lines of:

nn.ComputeOutputs(xValues);
double[] yValues = nn.GetOutputs();

One possible implementation of a GetOutputs method is:

public double[] GetOutputs()

{

  double[] result = new double[numOutput];

  for (int i = 0; i < numOutput; ++i)

    result[i] = this.outputs[i];

  return result;

}

Activation Functions

The demo program uses the hyperbolic tangent function for hidden layer node activation and the softmax function for output layer node activation. There is a third common activation function called the logistic sigmoid function. All three of these activation functions are closely related mathematically. From a developer's point of view, you need to know two things: when to use each activation function and how to implement each function.

Although there are some exceptions, in general the hyperbolic tangent function is the best choice for hidden layer activation. For output layer activation, if your neural network is performing classification where the dependent variable to be predicted has three or more values (for example, predicting a person's political inclination which can be "liberal", "moderate", or "conservative"), softmax activation is the best choice. If your neural network is performing classification where the dependent variable has exactly two possible values (for example, predicting a person's gender which can be "male" or "female"), the logistic sigmoid activation function is the best choice for output layer activation. Chapter 5 explains the details.

In the demo program, the hyperbolic tangent function is defined as:

private static double HyperTan(double v)

{

  if (v < -20.0)

    return -1.0;

  else if (v > 20.0)

    return 1.0;

  else

    return Math.Tanh(v);

}

Here the neural network HyperTan method is essentially a wrapper around the built-in .NET Tanh function. To better understand method HyperTan, take a look at the graph of the hyperbolic tangent shown in Figure 3-c. The Tanh function accepts any numeric value from negative infinity to positive infinity, and returns a value between -1.0 and +1.0. For example, Tanh(2.0) = 0.9640 and Tanh(-3.0) = -0.9951. Notice that for x values smaller than about -8.0 and larger than +8.0, the Tanh function result gets extremely close to -1 and +1 respectively.

Most programming languages, including C#, have a built-in hyperbolic tangent function. But in the early days of neural network research, some older programming languages had difficulty computing the hyperbolic tangent function for very small or very large input parameters. So, it was common to perform the kind of parameter check used in the HyperTan method.

The logistic sigmoid function, also called log-sigmoid, is similar to the hyperbolic tangent function. The logistic sigmoid function accepts any numeric value from negative infinity to positive infinity, and returns a value between 0.0 and +1.0. Unlike the hyperbolic tangent, most programming languages do not have a built-in logistic sigmoid function. The math definition of the logistic sigmoid function is: f(x) = 1 / (1 + e^-x).

Most programming languages, including C#, have a built-in function, usually named Exp, that returns e raised to a power. So, one possible implementation of the logistic sigmoid function is:

private static double LogSigmoid(double x)
{
  if (x < -45.0)
    return 0.0;
  else if (x > 45.0)
    return 1.0;
  else
    return 1.0 / (1.0 + Math.Exp(-x));
}

The input parameter check values of -45.0 and +45.0 are traditional values. On old computing hardware and software, the computation of Math.Exp(-x) could cause arithmetic overflow when x was very large or small, so the standard approach was to use an input parameter check.

Figure 3-c: The Hyperbolic Tangent Function

The softmax activation function is a variation of the logistic sigmoid function. The logistic sigmoid function accepts a single value and returns a single value between 0.0 and 1.0. The softmax activation function accepts n values and returns a set of n values which sum to 1.0. For example, softmax of { 1.0, 4.0, 2.0 } returns { 0.04, 0.84, 0.12 }.

The mathematical definition of the softmax function is a bit difficult to express, so an example may be the best way to explain. Suppose there are three values, 1.0, 4.0, and 2.0.

softmax(1.0) = e^1.0 / (e^1.0 + e^4.0 + e^2.0) = 2.7183 / (2.7183 + 54.5982 + 7.3891) = 0.04

softmax(4.0) = e^4.0 / (e^1.0 + e^4.0 + e^2.0) = 54.5982 / (2.7183 + 54.5982 + 7.3891) = 0.84

softmax(2.0) = e^2.0 / (e^1.0 + e^4.0 + e^2.0) = 7.3891 / (2.7183 + 54.5982 + 7.3891) = 0.12

A possible naive implementation of softmax is:

public static double[] SoftmaxNaive(double[] values)

{

  double denom = 0.0;

  for (int i = 0; i < oSums.Length; ++i)

    denom += Math.Exp(oSums[i]);

  double[] result = new double[oSums.Length];

  for (int i = 0; i < oSums.Length; ++i)

    result[i] = Math.Exp(oSums[i]) / denom;

  return result;

}

The problem with the naive implementation of the softmax function is that the denominator term can easily get very large or very small and cause a potential arithmetic overflow. It is possible to implement a more sophisticated version of the softmax function by using some clever math. Again, the technique is best explained by an example.

Using the three values from the previous example, 1.0, 4.0, and 2.0, the first step is to determine the largest value, which in this case is max = 4.0. The next step is to compute a scaling factor which is the sum of e raised to each input value minus the maximum input value:

scale =  e^{(1.0 - max)} + e^{(4.0 - max)} + e^{(2.0 - max)} = e^-3.0 + e⁰ + e^-2.0 = 0.0498 + 1 + 0.1353 = 1.1851

The final softmax outputs are e raised to each input minus the maximum divided by the scaling factor:

softmax(1.0)  =  e^{(1.0 - max)} / scale  =  e^-3.0 / 1.1851  = 0 .0498 / 1.1851  = 0.04

softmax(4.0)  =  e^{(4.0 - max)} / scale  =  e⁰ / 1.1851  = 1 / 1.1851  = 0.84

softmax(2.0)  =  e^{(2.0 - max)} / scale  =  e^-2.0 / 1.1851  = 0 .1353 / 1.1851  = 0.12

Notice that these are the same results as computed using the math definition. The reason why the two computation techniques give the same result isn't obvious, but is based on the property that e^{(a - b)} = e^a / e^b. The point of using the alternate computation technique is that the scaling process decreases the magnitude of each of the values that e is being raised to, which reduces the chances of arithmetic overflow. The demo program implementation of the softmax function is given in Listing 3-e.

Listing 3-e: The Softmax Activation Method

Because the softmax function is applied only to sums for output layer nodes, the method's input array parameter is named oSums rather than something more general like "values".

The demo program has hard-coded activation functions hyperbolic tangent for the hidden layer nodes, and softmax for the output layer nodes. An alternative is to pass some parameter information to the neural network constructor that indicates which activation function to use for each layer. This introduces additional complexity. As a rule of thumb, when I am developing code for my own use, I prefer simplicity over a more general solution. On the other hand, if you were developing neural network code for use by others, especially if you don't intend to make the source code available and editable, you'd have to take the general approach for dealing with activation functions.

There are many ways you could modify the neural network class presented here to handle parameterized activation functions. One approach is to define a class-scope enumeration type along with member fields, along the lines of:

public class NeuralNetwork

{

  public enum Activation { HyperTan, LogSigmoid, Softmax };

  private Activation hActivation;

  private Activation oActivation;

The constructor would accept additional parameters:

public NeuralNetwork(int numInput, int numHidden, int numOutput,

  Activation hActivation, Activation oActivation)

{

      this.numInput = numInput;

      this.numHidden = numHidden;

      this.numOutput = numOutput;

      this.hActivation = hActivation;

      this.oActivation = oActivation;

And the ComputeOutputs method could employ branching logic such as:

for (int i = 0; i < numHidden; ++i)

{

  if (this.hActivation == Activation.HyperTan)

    hOutputs[i] = HyperTan(hSums[i]);

  else if (this.hActivation == Activation.LogSigmoid)

    hOutputs[i] = LogSigmoid(hSums[i]);

}

The neural network constructor could then be called like:

NeuralNetwork nn = new NeuralNetwork(numInput, numHidden, numOutput,

  NeuralNetwork.Activation.HyperTan, NeuralNetwork.Activation.Softmax);

It should be apparent that designing a neural network to be general, typically for use by other developers, involves a lot of additional code. As you'll see in later chapters, there are dozens of ways to modify the behavior of a neural network. In general, I personally prefer to keep my neural network implementations as simple as possible and am willing to pay the price of having to modify source code often.

Complete Demo Program Source Code