k-Means Clustering

---

Introduction

Data clustering is the process of placing data items into groups so that similar items are in the same group (cluster) and dissimilar items are in different groups. After a data set has been clustered, it can be examined to find interesting patterns. For example, a data set of sales transactions might be clustered and then inspected to see if there are differences between the shopping patterns of men and women.

There are many different clustering algorithms. One of the most common is called the k-means algorithm. A good way to gain an understanding of the k-means algorithm is to examine the screenshot of the demo program shown in Figure 1-a. The demo program groups a data set of 10 items into three clusters. Each data item represents the height (in inches) and weight (in kilograms) of a person.

The data set was artificially constructed so that the items clearly fall into three distinct clusters. But even with only 10 simple data items that have only two values each, it is not immediately obvious which data items are similar:

(73.0, 72.6)
(61.0, 54.4)
(67.0, 99.9)
(68.0, 97.3)
(62.0, 59.0)
(75.0, 81.6)
(74.0, 77.1)
(66.0, 97.3)
(68.0, 93.3)
(61.0, 59.0)

However, after k-means clustering, it is clear that there are three distinct groups that might be labeled "medium-height and heavy", "tall and medium-weight", and "short and light":

(67.0, 99.9)
(68.0, 97.3)
(66.0, 97.3)
(68.0, 93.3)

(73.0, 72.6)
(75.0, 81.6)
(74.0, 77.1)

(61.0, 54.4)
(62.0, 59.0)
(61.0, 59.0)

The k-means algorithm works only with strictly numeric data. Each data item in the demo has two numeric components (height and weight), but k-means can handle data items with any number of values, for example, (73.0, 72.6, 98.6), where the third value is body temperature.

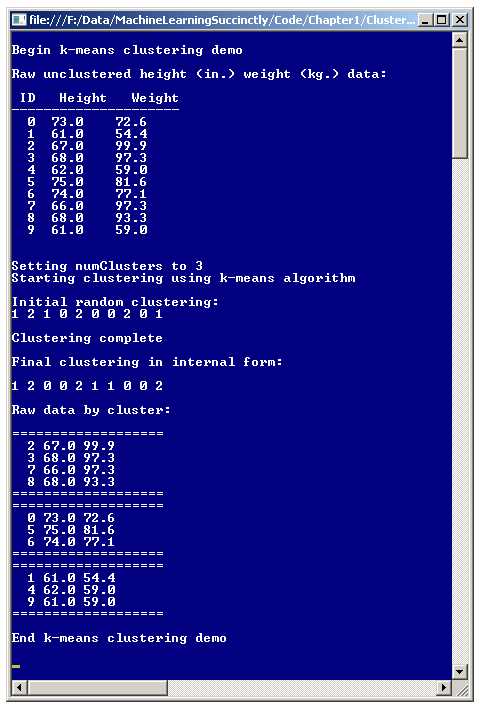
Figure 1-a: The k-Means Algorithm in Action

Notice that in the demo program, the number of clusters (the k in k-means) was set to 3. Most clustering algorithms, including k-means, require that the user specify the number of clusters, as opposed to the program automatically finding an optimal number of clusters. The k-means algorithm is an example of what is called an unsupervised machine learning technique because the algorithm works directly on the entire data set, without any special training items (with cluster membership pre-specified) required.

The demo program initially assigns each data tuple randomly to one of the three cluster IDs. After the clustering process finished, the demo displays the resulting clustering: { 1, 2, 0, 0, 2, 1, 1, 0, 0, 2 }, which means data item 0 is assigned to cluster 1, data item 1 is assigned to cluster 2, data item 2 is assigned to cluster 0, data item 3 is assigned to cluster 0, and so on.

Understanding the k-Means Algorithm

A naive approach to clustering numeric data would be to examine all possible groupings of the source data set and then determine which of those groupings is best. There are two problems with this approach. First, the number of possible groupings of a data set grows astronomically large, very quickly. For example, the number of ways to cluster n = 50 into k = 3 groups is:

119,649,664,052,358,811,373,730

Even if you could somehow examine one billion groupings (also called partitions) per second, it would take you well over three million years of computing time to analyze all possibilities. The second problem with this approach is that there are several ways to define exactly what is meant by the best clustering of a data set.

There are many variations of the k-means algorithm. The basic k-means algorithm, sometimes called Lloyd's algorithm, is remarkably simple. Expressed in high-level pseudo-code, k-means clustering is:

randomly assign all data items to a cluster
loop until no change in cluster assignments
  compute centroids for each cluster
  reassign each data item to cluster of closest centroid
end

Even though the pseudo-code is very short and simple, k-means is somewhat subtle and best explained using pictures. The left-hand image in Figure 1-b is a graph of the 10 height-weight data items in the demo program. Notice an optimal clustering is quite obvious. The right image in the figure shows one possible random initial clustering of the data, where color (red, yellow, green) indicates cluster membership.

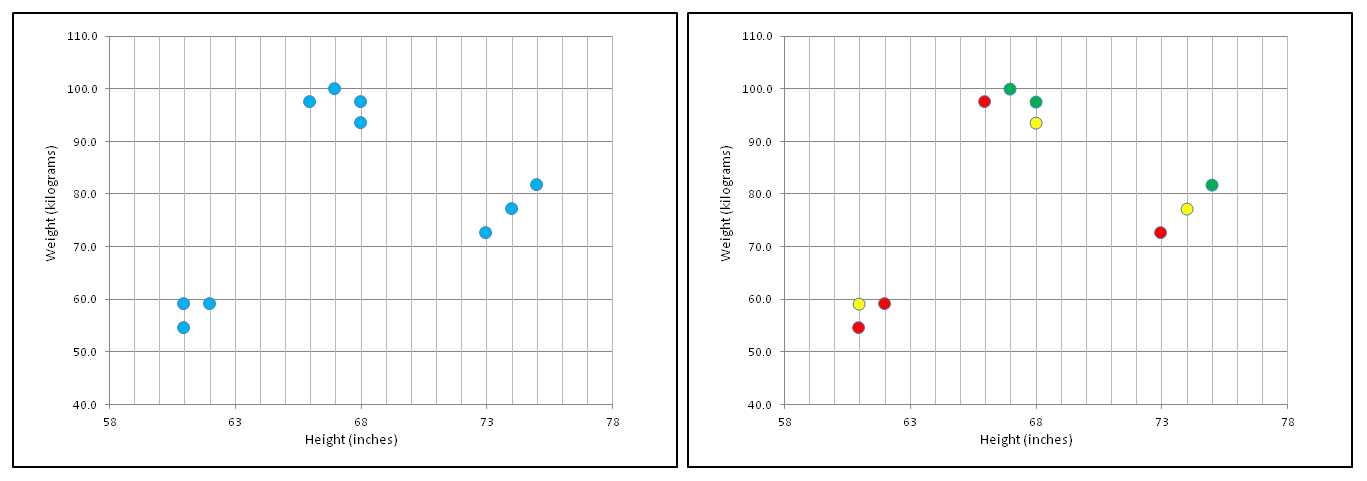
Figure 1-b: k-Means Problem and Cluster Initialization

After initializing cluster assignments, the centroids of each cluster are computed as shown in the left-hand graph in Figure 1-c. The three large dots are centroids. The centroid of the data items in a cluster is essentially an average item. For example, you can see that the four data items assigned to the red cluster are slightly to the left, and slightly below, the center of all the data points.

There are several other clustering algorithms that are similar to the k-means algorithm but use a different definition of a centroid item. This is why the k-means is named "k-means" rather than "k-centroids."

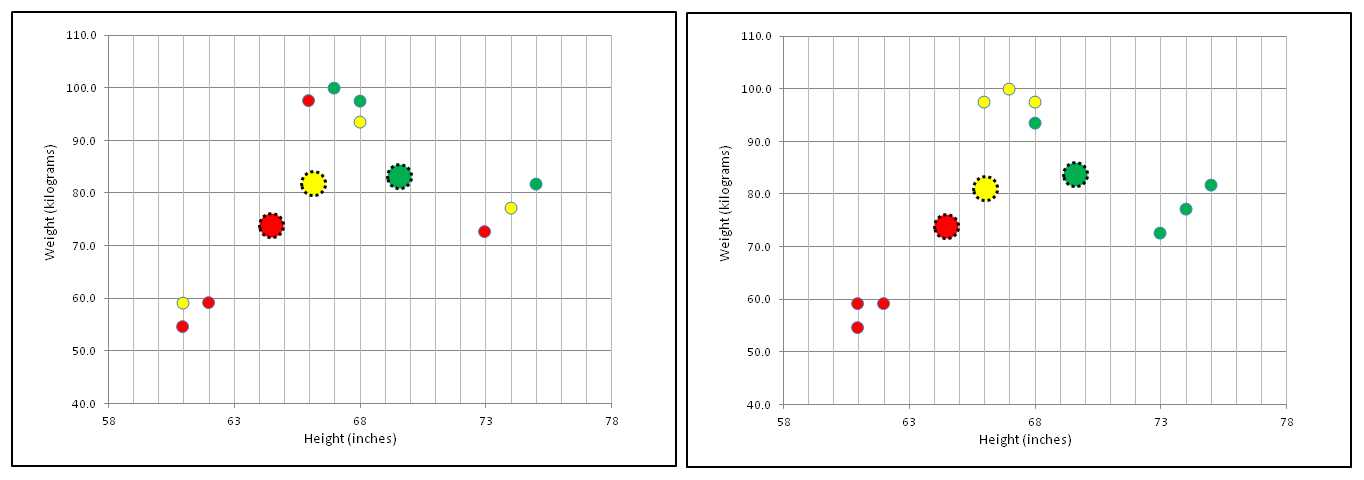
Figure 1-c: Compute Centroids and Reassign Clusters

After the centroids of each cluster are computed, the k-means algorithm scans each data item and reassigns each to the cluster that is associated with the closet centroid, as shown in the right-hand graph in Figure 1-c. For example, the three data points in the lower left part of the graph are clearly closest to the red centroid, so those three items are assigned to the red cluster.

The k-means algorithm continues iterating the update-centroids and update-clustering process as shown in Figure 1-d. In general, the k-means algorithm will quickly reach a state where there are no changes to cluster assignments, as shown in the right-hand graph in Figure 1-d.

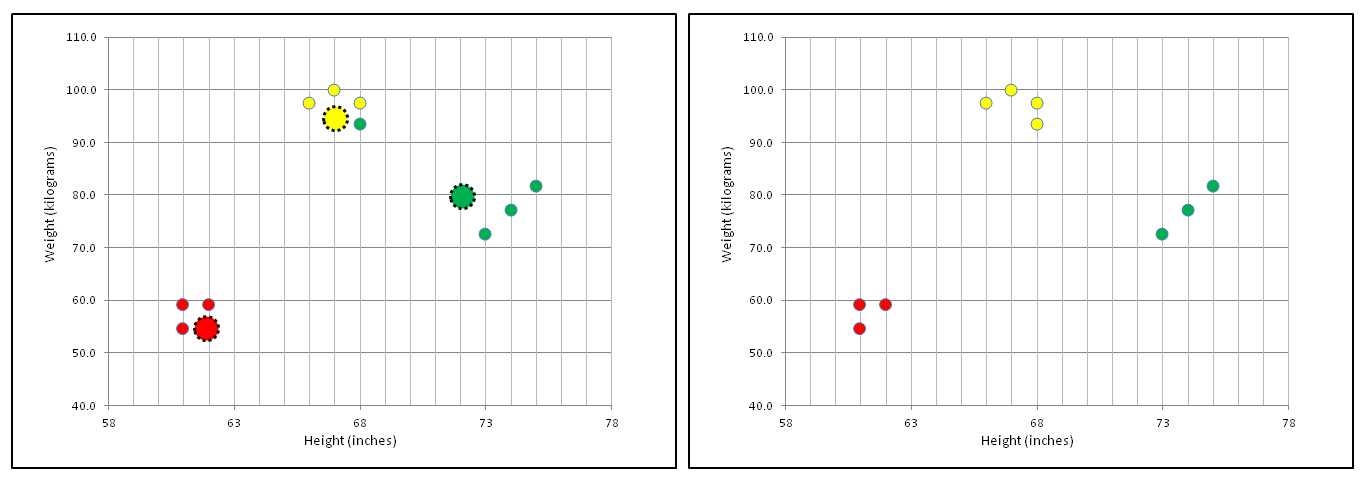
Figure 1-d: Update-Centroids and Update-Clustering Until No Change

The preceding explanation of the k-means algorithm leaves out some important details. For example, just how are data items initially assigned to clusters? Exactly what does it mean for a cluster centroid to be closest to a data item? Is there any guarantee that the update-centroids, update-clustering loop will exit?

Demo Program Overall Structure

To create the demo, I launched Visual Studio and selected the new C# console application template. The demo has no significant .NET version dependencies, so any version of Visual Studio should work.

After the template code loaded into the editor, I removed all using statements at the top of the source code, except for the single reference to the top-level System namespace. In the Solution Explorer window, I renamed the Program.cs file to the more descriptive ClusterProgram.cs, and Visual Studio automatically renamed class Program to ClusterProgram.

The overall structure of the demo program, with a few minor edits to save space, is presented in Listing 1-a. Note that in order to keep the size of the example code small, and the main ideas as clear as possible, the demo programs violate typical coding style guidelines and omit error checking that would normally be used in production code. The demo program class has three static helper methods. Method ShowData displays the raw source data items.

Listing 1-a: k-Means Demo Program Structure

Helper ShowVector displays the internal clustering representation, and method ShowClustered displays the source data after it has been clustered, grouped by cluster.

All the clustering logic is contained in a single program-defined class named Clusterer. All the program logic is contained in the Main method. The Main method begins by setting up 10 hard-coded, height-weight data items in an array-of-arrays style matrix:

static void Main(string[] args)

{

  Console.WriteLine("\nBegin k-means clustering demo\n");

  double[][] rawData = new double[10][];

  rawData[0] = new double[] { 73, 72.6 };

. . .

In a non-demo scenario, you would likely have data stored in a text file, and would load the data into memory using a helper function, as described in the next section. The Main method displays the raw data like so:

Console.WriteLine("Raw unclustered data:\n");

Console.WriteLine(" ID   Height (in.)   Weight (kg.)");

Console.WriteLine("---------------------------------");

ShowData(rawData, 1, true, true);

The four arguments to method ShowData are the matrix of type double to display, the number of decimals to display for each value, a Boolean flag to display indices or not, and a Boolean flag to print a final new line or not. Method ShowData is defined in Listing 1-b.

Listing 1-b: Displaying the Raw Data

One of many alternatives to consider is to pass to method ShowData an additional string array parameter named something like "header" that contains column names, and then use that information to display column headers.

In method Main, the calling interface to the clustering routine is very simple:

int numClusters = 3;

Console.WriteLine("\nSetting numClusters to " + numClusters);

Console.WriteLine("\nStarting clustering using k-means algorithm");

Clusterer c = new Clusterer(numClusters);

int[] clustering = c.Cluster(rawData);

Console.WriteLine("Clustering complete\n");

The program-defined Clusterer constructor accepts a single argument, which is the number of clusters to assign the data items to. The Cluster method accepts a matrix of data items and returns the resulting clustering in the form of an integer array, where the array index value is the index of a data item, and the array cell value is a cluster ID. In the screenshot in Figure 1-a, the return array has the following values:

{ 1, 2, 0, 0, 2, 1, 0, 0, 2 }

This means data item [0], which is (73.0, 72.6), is assigned to cluster 1, data [1] is assigned to cluster 2, data [2] is assigned to cluster 0, data [3] is assigned to cluster 0, and so on.

The Main method finishes by displaying the clustering, and displaying the source data grouped by cluster ID:

. . .

  Console.WriteLine("Final clustering in internal form:\n");

  ShowVector(clustering, true);

  Console.WriteLine("Raw data by cluster:\n");

  ShowClustered(rawData, clustering, numClusters, 1);

  Console.WriteLine("\nEnd k-means clustering demo\n");

  Console.ReadLine();

}

Helper method ShowVector is defined:

static void ShowVector(int[] vector, bool newLine)

{

  for (int i = 0; i < vector.Length; ++i)

    Console.Write(vector[i] + " ");

  if (newLine == true) Console.WriteLine("\n");

}

An alternative to relying on a static helper method to display the clustering result is to define a class ToString method along the lines of:

Console.WriteLine(c.ToString()); // display clustering[]

Helper method ShowClustered displays the source data in clustered form and is presented in Listing 1-c. Method ShowClustered makes multiple passes through the data set that has been clustered. A more efficient, but significantly more complicated alternative, is to define a local data structure, such as an array of List objects, and then make a first, single pass through the data, storing the clusterIDs associated with each data item. Then a second, single pass through the data structure could print the data in clustered form.

Listing 1-c: Displaying the Data in Clustered Form

An alternative to using a static method to display the clustered data is to implement a class member ToString method to do so.

Loading Data from a Text File

In non-demo scenarios, the data to be clustered is usually stored in a text file. For example, suppose the 10 data items in the demo program were stored in a comma-delimited text file, without a header line, named HeightWeight.txt like so:

73.0,72.6
61.0,54.4
. . .
61.0,59.0

One possible implementation of a LoadData method is presented in Listing 1-d. As defined, method LoadData accepts input parameters numRows and numCols for the number of rows and columns in the data file. In general, when working with machine learning, information like this is usually known.

Listing 1-d: Loading Data from a Text File

Calling method LoadData would look something like:

string dataFile = "..\\..\\HeightWeight.txt";
double[][] rawData = LoadData(dataFile, 10, 2, ',');

An alternative is to programmatically scan the data for the number of rows and columns. In pseudo-code it would look like:

numRows := 0

open file

while not EOF

  numRows := numRows + 1

end loop

close file

allocate result array with numRows

open file

while not EOF

  read and parse line with numCols

  allocate curr row of array with numCols

  store line

end loop

close file

return result matrix

Note that even if you are a very experienced programmer, unless you work with scientific or numerical problems often, you may not be familiar with C# array-of-arrays matrices. The matrix coding syntax patterns can take a while to become accustomed to.

The Key Data Structures

The important data structures for the k-means clustering program are illustrated in Figure 1-e. The array-of-arrays style matrix named data shows how the 10 height-weight data items (sometimes called data tuples) are stored in memory. For example, data[2][0] holds the height of the third person (67 inches) and data[2][1] holds the weight of the third person (99.9 kilograms). In code, data[2] represents the third row of the matrix, which is an array with two cells that holds the height and weight of the third person. There is no convenient way to access an entire column of an array-of-arrays style matrix.

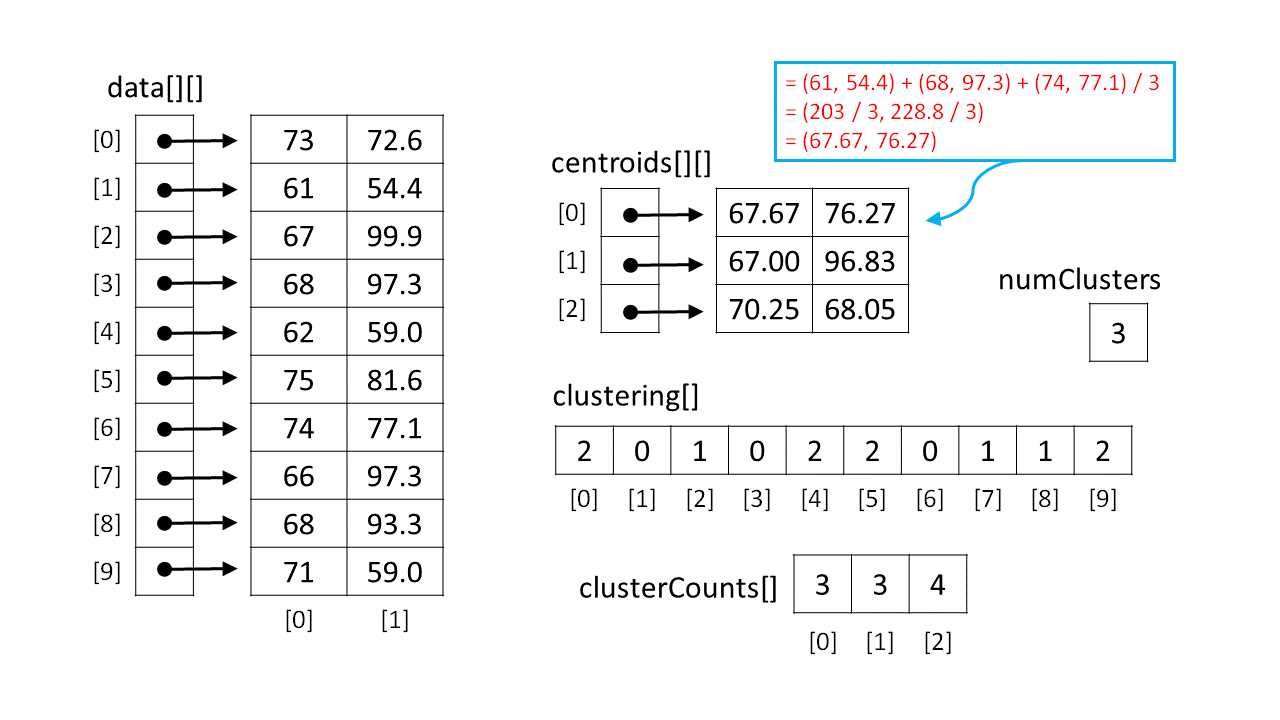
Figure 1-e: k-Means Key Data Structures

Unlike many programming languages, C# supports true, multidimensional arrays. For example, a matrix to hold the same values as the one shown in Figure 1-e could be declared and accessed like so:

double[,] data = new double[10,2]; // 10 rows, 2 columns
data[0,0] = 73;
data[0,1] = 72.6;

. . .

However, using array-of-arrays style matrices is much more common in C# machine learning scenarios, and is generally more convenient because entire rows can be easily accessed.

The demo program maintains an integer array named clustering to hold cluster assignment information. The array indices (0, 1, 2, 3, . . 9) represent indices of the data items. The array cell values { 2, 0, 1, . . 2 } represent the cluster IDs. So, in the figure, data item 0 (which is 73, 72.6) is assigned to cluster 2. Data item 1 (which is 61, 54.4) is assigned to cluster 0. And so on.

There are many alternative ways to store cluster assignment information that trade off efficiency and clarity. For example, you could use an array of List objects, where each List collection holds the indices of data items that belong to the same cluster. As a general rule, the relationship between a machine learning algorithm and the data structures used is very tight, and a change to one of the data structures will require significant changes to the algorithm code.

In Figure 1-e, the array clusterCounts holds the number of data items that are assigned to a cluster at any given time during the clustering process. The array indices (0, 1, 2) represent cluster IDs, and the cell values { 3, 3, 4 } represent the number of data items. So, cluster 0 has three data items assigned to it, cluster 1 also has three items, and cluster 2 has four data items.

In Figure 1-e, the array-of-arrays matrix centroids holds what you can think of as average data items for each cluster. For example, the centroid of cluster 0 is { 67.67, 76.27 }. The three data items assigned to cluster 0 are items 1, 3, and 6, which are { 61, 54.4 }, { 68, 97.3 } and      { 74, 77.1 }. The centroid of a set of vectors is just a vector where each component is the average of the set's values. For example:

centroid[0] = (61 + 68 + 74) / 3 , (54.4 + 97.3 + 77.1) / 3
                  = 203 / 3 , 228.8 / 3
                  = (67.67, 76.27)

Notice that like the close relationship between an algorithm and the data structures used, there is a very tight coupling among the key data structures. Based on my experience with writing machine learning code, it is essential (for me at least) to have a diagram of all data structures used. Most of the coding bugs I generate are related to the data structures rather than the algorithm logic.

The Clusterer Class

A program-defined class named Clusterer houses the k-means clustering algorithm code. The structure of the class is presented in Listing 1-e.

Listing 1-e: Program-Defined Clusterer Class

Class Clusterer has four data members, two public methods, and six private helper methods. Three of four data members—variable numClusters, array clustering, and matrix centroids—are explained by the diagram in Figure 1-e. The fourth data member, rnd, is a Random object used during the k-means initialization process.

Data member rnd is used to generate pseudo-random numbers when data items are initially assigned to random clusters. In most clustering scenarios there is just a single clustering object, but if multiple clustering objects are needed, you may want to consider decorating data member rnd with the static keyword so that there is just a single random number generator shared between clustering object instances.

Class Clusterer exposes just two public methods: a single class constructor, and a method Cluster. Method Cluster calls private helper methods InitRandom, UpdateCentroids, and UpdateClustering. Helper method UpdateClustering calls sub-helper static methods Distance and MinIndex.

The class constructor is short and straightforward:

public Clusterer(int numClusters)

{

  this.numClusters = numClusters;

  this.centroids = new double[numClusters][];

  this.rnd = new Random(0);

}

The single input parameter, numClusters, is assigned to the class data member of the same name. You may want to perform input error checking to make sure the value of parameter numClusters is greater than or equal to 2. The ability to control when to omit error checking to improve performance is an advantage of writing custom machine learning code.

The constructor allocates the rows of the data member matrix centroids, but cannot allocate the columns because the number of columns will not be known until the data to be clustered is presented. Similarly, array clustering cannot be allocated until the number of data items is known. The Random object is initialized with a seed value of 0, which is arbitrary. Different seed values can produce significantly different clustering results. A common design option is to pass the seed value as an input parameter to the constructor.

If you refer back to Listing 1-a, the key calling code is:

int numClusters = 3;
Clusterer c = new Clusterer(numClusters);
int[] clustering = c.Cluster(rawData);

Notice the Clusterer class does not learn about the data to be clustered until that data is passed to the Cluster method. An important alternative design is to include a reference to the data to be clustered as a class member, and pass the reference to the class constructor. In other words, the Clusterer class would contain an additional field:

private double[][] rawData;

And the constructor would then be:

public Clusterer(int numClusters, double[][] rawData)
{
  this.numClusters = numClusters;
  this.rawData = rawData;
  . . .
}

The pros and cons of this design alternative are a bit subtle. One advantage of including the data to be clustered is that it leads to a slightly cleaner design. In my opinion, the two design approaches have roughly equal merit. The decision of whether to pass data to a class constructor or to a public method is a recurring theme when creating custom machine learning code.

The Cluster Method

Method Cluster is presented in Listing 1-f. The method accepts a reference to the data to be clustered, which is stored in an array-of-arrays style matrix.

Listing 1-f: The Cluster Method

The definition of method Cluster begins with:

public int[] Cluster(double[][] data)
{
  int numTuples = data.Length;

  int numValues = data[0].Length;

  this.clustering = new int[numTuples];

. . .

The first two statements determine the number of data items to be clustered and the number of values in each data item. Strictly speaking, these two variables are unnecessary, but using them makes the code somewhat easier to understand. Recall that class member array clustering and member matrix centroids could not be allocated in the constructor because the size of the data to be clustered was not known. So, clustering and centroids are allocated in method Cluster when the data is first known.

Next, the columns of the data member matrix centroids are allocated:

for (int k = 0; k < numClusters; ++k)

  this.centroids[k] = new double[numValues];

Here, class member centroids is referenced using the this keyword, but member numClusters is referenced without the keyword. In a production environment, you would likely use a standardized coding style.

Next, method Cluster initializes the clustering with random assignments by calling helper method InitRandom:

InitRandom(data);

Console.WriteLine("\nInitial random clustering:");

for (int i = 0; i < clustering.Length; ++i)

  Console.Write(clustering[i] + " ");

Console.WriteLine("\n");

The k-means initialization process is a major customization point and will be discussed in detail shortly. After the call to InitRandom, the demo program displays the initial clustering to the command shell purely for demonstration purposes. The ability to insert display statements anywhere is another advantage of writing custom machine learning code, compared to using an existing tool or API set where you don't have access to source code.

The heart of method Cluster is the update-centroids, update-clustering loop:

bool changed = true;

int maxCount = numTuples * 10; // sanity check

int ct = 0;

while (changed == true && ct <= maxCount)

{

  ++ct;

  UpdateCentroids(data);

  changed = UpdateClustering(data);

}

Helper method UpdateCentroids uses the current clustering to compute the centroid for each cluster. Helper method UpdateClustering then uses the new centroids to reassign each data item to the cluster that is associated with the closest centroid. The method returns false if no data items change clusters.

The k-means algorithm typically reaches a stable clustering very quickly. Mathematically, k-means is guaranteed to converge to a local optimum solution. But this fact does not mean that an implementation of the clustering process is guaranteed to terminate. It is possible, although extremely unlikely, for the algorithm to oscillate, where one data item is repeatedly swapped between two clusters. To prevent an infinite loop, a sanity counter is maintained. Here, the maximum loop count is set to numTuples * 10, which is sufficient in most practical scenarios.

Method Cluster finishes by copying the values in class member array clustering into a local return array. This allows the calling code to access and view the clustering without having to implement a public method along the lines of a routine named GetClustering.

. . .

  int[] result = new int[numTuples];

  Array.Copy(this.clustering, result, clustering.Length);

  return result;

}

You might want to consider checking the value of variable ct before returning the clustering result. If the value of variable ct equals the value of maxCount, then method Cluster terminated before reaching a stable state, which likely indicates something went very wrong.

Clustering Initialization

The initialization process is critical to the k-means algorithm. After initialization, clustering is essentially deterministic, so a k-means clustering result depends entirely on how the clustering is initialized. There are two main initialization approaches. The demo program assigns each data tuple to a random cluster ID, making sure that each cluster has at least one tuple assigned to it. The definition of method InitRandom begins with:

private void InitRandom(double[][] data)

{

  int numTuples = data.Length;

  int clusterID = 0;

  for (int i = 0; i < numTuples; ++i)

  {

    clustering[i] = clusterID++;

    if (clusterID == numClusters)

      clusterID = 0;

  }

. . .

The idea is to make sure that each cluster has at least one data tuple assigned. For the demo data with 10 tuples, the code here would initialize class member array clustering to { 0, 1, 2, 0, 1, 2, 0, 1, 2, 0 }. This semi-random initial assignment of data tuples to clusters is fine for most purposes, but it is normal to then further randomize the cluster assignments like so:

  for (int i = 0; i < numTuples; ++i)

  {

    int r = rnd.Next(i, clustering.Length); // pick a cell

    int tmp = clustering[r]; // get the cell value

    clustering[r] = clustering[i]; // swap values

    clustering[i] = tmp;

  }

} // InitRandom

This randomization code uses an extremely important mini-algorithm called the Fisher-Yates shuffle. The code makes a single scan through the clustering array, swapping pairs of randomly selected values. The algorithm is quite subtle. A common mistake in Fisher-Yates is:

int r = rnd.Next(0, clustering.Length); // wrong!

Although it is not obvious at all, the bad code generates an apparently random ordering of array values, but in fact the ordering would be strongly biased toward certain patterns.

The second main k-means clustering initialization approach is sometimes called Forgy initialization. The idea is to pick a few actual data tuples to act as initial pseudo-means, and then assign each data tuple to the cluster corresponding to the closest pseudo-mean. In my opinion, research results are not conclusive about which clustering initialization approach is better under which circumstances.

Updating the Centroids

The code for method UpdateClustering begins by computing the current number of data tuples assigned to each cluster:

private bool UpdateCentroids(double[][] data)

{

  int[] clusterCounts = new int[numClusters];

  for (int i = 0; i < data.Length; ++i)

  {

    int clusterID = clustering[i];

    ++clusterCounts[clusterID];

  }
. . .

The number of tuples assigned to each cluster is needed to compute the average of each centroid component. Here, the clusterCounts array is declared local to method UpdateCentroids. An alternative is to declare clusterCounts as a class member. When writing object-oriented code, it is sometimes difficult to choose between using class members or local variables, and there are very few good, general rules-of-thumb in my opinion.

Next, method UpdateClustering zeroes-out the current cells in the this.centroids matrix:

for (int k = 0; k < centroids.Length; ++k)

  for (int j = 0; j < centroids[k].Length; ++j)

    centroids[k][j] = 0.0;

An alternative is to use a scratch matrix to perform the calculations. Next, the sums are accumulated:

for (int i = 0; i < data.Length; ++i)

{

  int clusterID = clustering[i];

  for (int j = 0; j < data[i].Length; ++j)

    centroids[clusterID][j] += data[i][j]; // accumulate sum

}

Even though the code is short, it's a bit tricky and, for me at least, the only way to fully understand what is going on is to sketch a diagram of the data structures, like the one shown in Figure 1-e. Method UpdateCentroids concludes by dividing the accumulated sums by the appropriate cluster count:

. . .

  for (int k = 0; k < centroids.Length; ++k)

    for (int j = 0; j < centroids[k].Length; ++j)

      centroids[k][j] /= clusterCounts[k]; // danger?

} // UpdateCentroids

Notice that if any cluster count has the value 0, a fatal division by zero error will occur. Recall the basic k-means algorithm is:

initialize clustering
loop
  update centroids
  update clustering
end loop

This implies it is essential that the cluster initialization and cluster update routines ensure that no cluster counts ever become zero. But how can a cluster count become zero? During the k-means processing, data tuples are reassigned to the cluster that corresponds to the closest centroid. Even if each cluster initially has at least one tuple assigned to it, if a data tuple is equally close to two different centroids, the tuple may move to either associated cluster.

Updating the Clustering

The definition of method UpdateClustering starts with:

private bool UpdateClustering(double[][] data)

{

  bool changed = false;

  int[] newClustering = new int[clustering.Length];

  Array.Copy(clustering, newClustering, clustering.Length);

  double[] distances = new double[numClusters];

. . .

Local variable changed holds the method return value; it's assumed to be false and will be set to true if any tuple changes cluster assignment. Local array newClustering holds the proposed new clustering. The local array named distances holds the distance from a given data tuple to each centroid. For example, if array distances held { 4.0, 1.5, 2.8 }, then the distance from some tuple to cluster 0 is 4.0, the distance from the tuple to centroid 1 is 1.5, and the distance from the tuple to centroid 2 is 2.8. Therefore, the tuple is closest to centroid 1 and would be assigned to cluster 1.

Next, method UpdateClustering does just that with the following code:

for (int i = 0; i < data.Length; ++i) // each tuple

{

  for (int k = 0; k < numClusters; ++k)

    distances[k] = Distance(data[i], centroids[k]);

  int newClusterID = MinIndex(distances); // closest centroid

  if (newClusterID != newClustering[i])

  {

    changed = true; // note a new clustering

    newClustering[i] = newClusterID; // accept update

  }

}

The key code calls two helper methods: Distance, to compute the distance from a tuple to a centroid, and MinIndex, to identify the cluster ID of the smallest distance. Next, the method checks to see if any data tuples changed cluster assignments:

if (changed == false)

  return false;

If there is no change to the clustering, then the algorithm has stabilized and UpdateClustering can exit with the current clustering. Another early exit occurs if the proposed new clustering would result in a clustering where one or more clusters have no data tuples assigned to them:

int[] clusterCounts = new int[numClusters];

for (int i = 0; i < data.Length; ++i)

{

  int clusterID = newClustering[i];

  ++clusterCounts[clusterID];

}

for (int k = 0; k < numClusters; ++k)

  if (clusterCounts[k] == 0)

    return false; // bad proposed clustering

Exiting early when the proposed new clustering would produce an empty cluster is simple and effective, but could lead to a mathematically non-optimal clustering result. An alternative approach is to move a randomly selected data item from a cluster with two or more assigned tuples to the empty cluster. The code to do this is surprisingly tricky. The demo program listing at the end of this chapter shows one possible implementation.

Method UpdateClustering finishes by transferring the values in the proposed new clustering, which is now known to be good, into the class member clustering array and returning Boolean true, indicating there was a change in cluster assignments:

. . .

  Array.Copy(newClustering, this.clustering, newClustering.Length);

  return true;

} // UpdateClustering

Helper method Distance is short but significant:

private static double Distance(double[] tuple, double[] centroid)

{

  double sumSquaredDiffs = 0.0;

  for (int j = 0; j < tuple.Length; ++j)

    sumSquaredDiffs += (tuple[j] - centroid[j]) * (tuple[j] - centroid[j]);

  return Math.Sqrt(sumSquaredDiffs);

}

Method Distance computes the Euclidean distance between a data tuple and a centroid. For example, suppose some tuple is (70, 80.0) and a centroid is (66, 83.0). The Euclidean distance is:

distance = Sqrt( (70 - 66)² + (80.0 - 83.0)² )
               = Sqrt( 16 + 9.0 )
               = Sqrt( 25.0 )
               = 5.0

There are several alternatives to the Euclidean distance that can be used with the k-means algorithm. One of the common alternatives you might want to investigate is called the cosine distance.

Helper method MinIndex locates the index of the smallest value in an array. For the k-means algorithm, this index is equivalent to the cluster ID of the closest centroid:

private static int MinIndex(double[] distances)

{

  int indexOfMin = 0;

  double smallDist = distances[0];

  for (int k = 1; k < distances.Length; ++k)

  {

    if (distances[k] < smallDist)

    {

      smallDist = distances[k];

      indexOfMin = k;

    }

  }

  return indexOfMin;

}

Even a short and simple routine like method MinIndex has some implementation alternatives to consider. For example, if the method's static qualifier is removed, then the reference to distances.Length can be replaced with this.numClusters.

Summary

The k-means algorithm can be used to group numeric data items. Although it is possible to apply k-means to categorical data by first transforming the data to a numeric form, k-means is not a good choice for categorical data clustering. The main problem is that k-means relies on the notion of distance, which makes sense for numeric data, but usually doesn't make sense for a categorical variable such as color that can take values like red, yellow, and pink.

One important option not presented in the demo program is to normalize the data to be clustered. Normalization transforms the data so that the values in each column have roughly similar magnitudes. Without normalization, columns that have very large magnitude values can dominate columns with small magnitude values. The demo program did not need normalization because the magnitudes of the column values—height in inches and weight in kilograms—were similar.

An algorithm that is closely related to k-means is called k-medoids. Recall that in k-means, a centroid for each cluster is computed, where each centroid is essentially an average data item. Then, each data item is assigned to the cluster associated with the closet centroid. In k-medoids clustering, centroids are calculated, but instead of being an average data item, each centroid is required to be one of the actual data items. Another closely related algorithm is called k-medians clustering. Here, the centroid of each cluster is the median of the data items in the cluster, rather than the average of the data items in the cluster.

Chapter 1 Complete Demo Program Source Code