Categorical Data Clustering

---

Introduction

Data clustering is the process of placing data items into different groups (clusters) in such a way that items in a particular cluster are similar to each other and items in different clusters are different from each other. Once clustered, the data can be examined to find useful information, such as determining what types of items are often purchased together so that targeted advertising can be aimed at customers.

The most common clustering technique is the k-means algorithm. However, k-means is really only applicable when the data items are completely numeric. Clustering data sets that contain categorical attributes such as color, which can take on values like "red" and "blue", is a challenge. One of several approaches for clustering categorical data, or data sets that contain both numeric and categorical data, is to use a concept called category utility (CU).

The CU value for a set of clustered data is a number like 0.3299 that is a measure of how good the particular clustering is. Larger values of CU are better, where the clustering is less likely than a random clustering of the data. There are several clustering algorithms based on CU. This chapter describes a technique called greedy agglomerative category utility clustering (GACUC).

A good way to get a feel for the GACUC clustering algorithm is to examine the screenshot of the demo program shown in Figure 2-a. The demo program clusters a data set of seven items into two groups. Each data item represents a gemstone. Each item has three attributes: color (red, blue, green, or yellow), size (small, medium, or large), and heaviness (false or true).

The final clustering of the seven data items is:

Index  Color    Size     Heavy
-------------------------------
0     Blue     Small    False
2     Red      Large    False
3     Red      Small    True
6     Red      Large    False
-------------------------------
1     Green    Medium   True
4     Green    Medium   False
5     Yellow   Medium   False
-------------------------------
CU = 0.3299

Even though it's surprisingly difficult to describe exactly what a good clustering is, most people would likely agree that the final clustering shown is the best way to place the seven data items into two clusters.

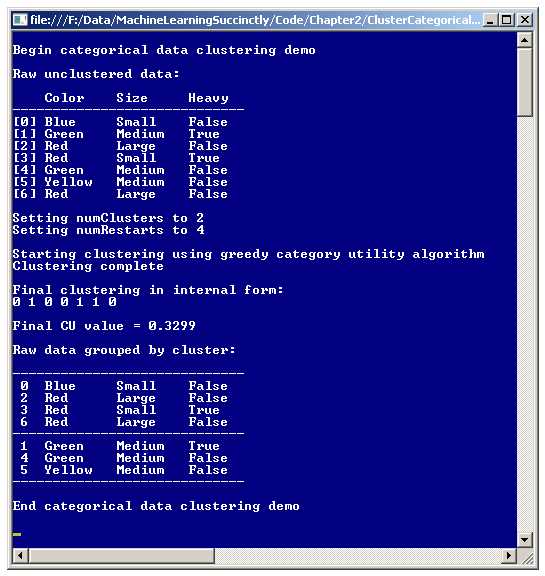
Figure 2-a: Clustering Categorical Data

Clustering using the GACUC algorithm, like most clustering algorithms, requires the user to specify the number of clusters in advance. However, unlike most clustering algorithms, GACUC provides a metric of clustering goodness, so you can try clustering with different numbers of clusters and easily compare the results.

Understanding Category Utility

The key to implementing and customizing the GACUC clustering algorithm is understanding category utility. Data clustering involves solving two main problems. The first problem is defining exactly what makes a good clustering of data. The second problem is determining an effective technique to search through all possible combinations of clustering to find the best clustering.

CU addresses the first problem. CU is a very clever metric that defines a clustering goodness. Small values of CU indicate poor clustering and larger values indicate better clustering. As far as I've been able to determine, CU was first defined by M. Gluck and J. Corter in a 1985 research paper titled "Information, Uncertainty, and the Utility of Categories."

The mathematical equation for CU is a bit intimidating at first glance:

The equation is simpler than it first appears. Uppercase C is an overall clustering. Lowercase m is the number of clusters. Lowercase k is a zero-based cluster index. Uppercase P means "probability of." Uppercase A means attribute (such as color). Uppercase V means attribute value (such as red).

The term inside the double summation on the right represents the probability of guessing an attribute value purely by chance. The term inside the double summation on the left represents the probability of guessing an attribute value for the given clustering. So, the larger the difference, the less likely the clustering occurred by chance.

Computing category utility is probably best understood by example. Suppose the data set to be clustered is the one shown at the top of Figure 2-a, and you want to compute the CU of this (non-best) clustering:

k = 0
------------------------
Red      Large    False
Green    Medium   False
Yellow   Medium   False
Red      Large    False

k = 1
------------------------
Blue     Small    False
Green    Medium   True
Red      Small    True

The first step is to compute the P(C_k), which are the probabilities of each cluster. For k = 0, because there are seven tuples in the data set and four of them are in cluster 0, P(C₀) = 4/7 = 0.5714. Similarly, P(C₁) = 3/7 = 0.4286.

The second step is to compute the double summation on the right in the CU equation, called the unconditional term. The computation is the sum of N terms where N is the total number of different attribute values in the data set, and goes like this:

Red:    (3/7)² = 0.1837

Blue:   (1/7)² = 0.0204

Green:  (2/7)² = 0.0816

Yellow: (1/7)² = 0.0204

Small:  (2/7)² = 0.0816

Medium: (3/7)² = 0.1837

Large:  (2/7)² = 0.0816

False:  (5/7)² = 0.5102

True:   (2/7)² = 0.0816

Unconditional sum = 0.1837 + 0.0204 + . . . + 0.0816 = 1.2449 (rounded)

The third step is to compute the double summation on the left, called the conditional probability terms. There are m sums (where m is the number of clusters), each of which has N terms.

For k = 0 the computation goes:

Red:    (2/4)² = 0.2500
Blue:   (0/4)² = 0.0000
Green:  (1/4)² = 0.0625
Yellow: (1/4)² = 0.0625
Small:  (0/4)² = 0.0000
Medium: (2/4)² = 0.2500
Large:  (2/4)² = 0.2500
False:  (4/4)² = 1.0000
True:   (0/4)² = 0.0000

Conditional k = 0 sum = 0.2500 + 0.0000 + . . . + 0.2500 = 1.8750

For k = 1 the computation is:

Red:    (1/3)² = 0.1111
Blue:   (1/3)² = 0.1111
Green:  (1/3)² = 0.1111
Yellow: (0/3)² = 0.0000
Small:  (2/3)² = 0.4444
Medium: (1/3)² = 0.1111
Large:  (0/3)² = 0.0000
False:  (1/3)² = 0.1111
True:   (2/3)² = 0.4444

Conditional k = 1 sum = 0.1111 + 0.1111 + . . . + 0.4444 = 1.4444 (rounded)

The last step is to combine the computed sums according to the CU equation:

CU = 1/2 * [ 0.5714 * (1.8750 - 1.2449) + 0.4286 * (1.4444 - 1.2449) ]

      = 0.2228 (rounded)

Notice the CU of this non-optimal clustering, 0.2228, is less than the CU of the optimal clustering, 0.3299, shown in Figure 2-a. The key point is that for any clustering of a data set containing categorical data, it is possible to compute a value that describes how good the clustering is.

Understanding the GACUC Algorithm

After defining a way to measure clustering goodness, the second challenging step when clustering categorical data is coming up with a technique to search through all possible clusterings. In general, it is not feasible to examine every possible clustering of a data set. For example, even for a data set with only 100 tuples, and m = 2 clusters, there are 2¹⁰⁰ / 2! = 2⁹⁹ = 633,825,300,114,114,700,748,351,602,688 possible clusterings. Even if you could somehow examine one trillion clusterings per second, it would take roughly 19 billion years to check them all. For comparison, the age of the universe is estimated to be about 14 billion years.

The GACUC algorithm uses what is called a greedy agglomerative approach. The idea is to begin by seeding each cluster with a single data tuple. Then for each remaining tuple, determine which cluster, if the current tuple were added to it, would yield the best overall clustering. Then the tuple that gives the best CU is actually assigned to that cluster.

Expressed in pseudo-code:

assign just one data tuple to each cluster
loop each remaining tuple
  for each cluster
    compute CU if tuple were to be assigned to cluster
    save proposed CU
  end for
  determine which cluster assignment would have given best CU
  actually assign tuple to that cluster
end loop

The algorithm is termed greedy because the best choice (tuple-cluster assignment in this case) at any given state is always selected. The algorithm is termed agglomerative because the final solution (overall clustering in this case) is built up one item at a time.

This algorithm does not guarantee that the optimal clustering will be found. The final clustering produced by the GACUC algorithm depends on which m tuples are selected as initial seed tuples, and the order in which the remaining tuples are examined. But because the result of any clustering has a goodness metric, CU, you can use what is called “restart”. In pseudo-code:

loop n times
  cluster all data tuples, computing the current CU
  if current CU > best CU
    save current clustering
    best CU := current CU
  end if
end loop
return best clustering found

It turns out that selecting an initial data tuple for each cluster is not trivial. One naive approach would be to simply select m random tuples as the seeds. However, if the seed tuples are similar to each other, then the resulting clustering could be poor. A better approach for selecting initial tuples for each cluster is to select m tuples that are as different as possible from each other.

There are several ways to define how a set of data tuples differ. The simplest approach is to count the total number of attribute values that differ when each possible pair of tuples is examined. This is called the Hamming distance. For example, consider these three tuples:

[0]  Red      Large    False
[1]  Green    Medium   False
[2]  Yellow   Medium   False

Looking at the color attribute, items 0 and 1 differ, 0 and 2 differ, and 1 and 2 differ. Looking at the size attribute, items 0 and 1 differ, and items 0 and 2 differ. Looking at the heaviness attribute, no pairs of tuples differ. So there are a total of 3 + 2 + 0 = 5 differences. Larger values for the difference metric mean more dissimilarity, which is better for choosing the initial tuples to be assigned to clusters.

Now another, but relatively minor, problem arises. In most situations it isn't feasible to examine all possible sets of initial tuples. If there are T data tuples and m clusters, then there are Choose(T, m) ways to select m tuples from the set of T tuples. For example, if T = 500 and m = 10, then there are Choose(500, 10) = 500! / 10! * 490! = 245,810,588,801,891,098,700 possible sets of initial tuples to examine. GACUC uses this approach to select a few random sets of initial tuples to examine, rather than try to examine all possible sets.

Demo Program Overall Structure

To create the demo, I launched Visual Studio and created a new C# console application and named it ClusterCategorical. After the template code loaded in the editor, I removed all using statements at the top of the source code, except for the references to the top-level System and the Collections.Generic namespaces.

In the Solution Explorer window, I renamed file Program.cs to the more descriptive ClusterCatProgram.cs, and Visual Studio automatically renamed class Program to ClusterCatProgram.

The overall structure of the demo program, with a few minor edits to save space, is presented in Listing 2-a. Note that in order to keep the size of the example code small, and the main ideas as clear as possible, all normal error checking is omitted.

Listing 2-a: Categorical Data Clustering Demo Program Structure

All the clustering logic is contained in a single program-defined class named CatClusterer. All the program logic is contained in the Main method. The Main method begins by setting up seven hard-coded, color-size-heaviness data items in an array-of-arrays style matrix:

static void Main(string[] args)

{

  Console.WriteLine("\nBegin categorical data clustering demo\n");

  string[][] rawData = new string[7][];

  rawData[0] = new string[] { "Blue", "Small", "False" };

  rawData[1] = new string[] { "Green", "Medium", "True" };

  rawData[2] = new string[] { "Red", "Large", "False" };

  rawData[3] = new string[] { "Red", "Small", "True" };

  rawData[4] = new string[] { "Green", "Medium", "False" };

  rawData[5] = new string[] { "Yellow", "Medium", "False" };

  rawData[6] = new string[] { "Red", "Large", "False" };

. . .

In a non-demo scenario, you would likely have data stored in a text file and would load the data into memory using a helper function. After displaying the raw string data matrix using helper method ShowData, the demo program prepares the clustering parameters:

int numClusters = 2;

Console.WriteLine("\nSetting numClusters to " + numClusters);

int numRestarts = 4;

Console.WriteLine("Setting numRestarts to " + numRestarts);

Variable numRestarts holds the number of times the GACUC algorithm will be called, looking for the clustering that gives the largest CU value. Larger values of numRestarts increase the chances of finding the optimal clustering, but at the expense of time. A rule of thumb that often works well in practice is to set numRestarts to the square root of the number of data items.

The calling interface is simple:

CatClusterer cc = new CatClusterer(numClusters, rawData);

double cu;

int[] clustering = cc.Cluster(numRestarts, out cu);

ShowVector(clustering, true);

Console.WriteLine("Final CU value = " + cu.ToString("F4"));

A CatClusterer object is instantiated and its Cluster method is called. Behind the scenes, method Cluster calls a method ClusterOnce several (numRestarts) times, keeping track of the best clustering found. That best clustering, and its associated CU value, are returned.

In the demo program, the final best clustering is stored into an array called clustering and is encoded as { 0, 1, 0, 0, 1, 1, 0 }. This means data tuple 0 is assigned to cluster 0, data tuple 1 is assigned to cluster 1, data tuple 2 is assigned to cluster 0, and so on. The final CU value of the best clustering found is stored into out-parameter cu and is 0.3299.

The demo program concludes by calling helper method ShowClustering to display the raw data, arranged by cluster:

. . .
  Console.WriteLine("\nRaw data grouped by cluster:\n");
  ShowClustering(numClusters, clustering, rawData);
  Console.WriteLine("\nEnd categorical data clustering demo\n");
  Console.ReadLine();
} // Main

The Key Data Structures

The important data structures for the GACUC categorical data clustering program are illustrated in Figure 2-b. The array-of-arrays style matrix named rawData shows the data tuples where attribute values (like red) are in string form. Matrix tuplesAsInt holds the same data but where each attribute value has been converted to a zero-based index (like 2). In situations with very large data sets or limited machine memory, an alternative design is to store string-to-integer encoding, for example, by using a generic Dictionary collection for each attribute column.

The GACUC algorithm computes category utility many times. It would be possible to compute CU from scratch each time, which would involve scanning the entire data set and counting the number of attribute values assigned to each cluster. But a far more efficient approach is to store the current count of each attribute value in a data structure, and then update the data structure as each data tuple is assigned to a cluster. Data structure valueCounts stores this information.

The first index of valueCounts is an attribute, like color. The second index is an attribute value, like red. The third index is a cluster ID, like 0. The cell value is the count. For example, if cell valueCounts[0][2][0] has value 3, this means there are three data tuples assigned to cluster 0,  where color (0) has value red (2).

The cell in valueCounts where the third index has value numClusters holds the sum of assigned tuples for all clusters for the associated attribute value. For example, valueCounts[0][2][2] holds the number of tuples assigned where color = red.

Figure 2-b: GACUC Clustering Algorithm Key Data Structures

The array clusterCounts holds the number of data tuples assigned to each cluster at any point during the algorithm, and also the total number of tuples that have been assigned. For example, if clusterCounts has values { 2, 3, 5 }, then two tuples have been assigned to cluster 0, three tuples have been assigned to cluster 1, and a total of five tuples have been assigned.

The CatClusterer Class

A program-defined class named CatClusterer houses the GACUC algorithm code. The structure of the class is presented in Listing 2-b.

Listing 2-b: Program-Defined CatClusterer Class

Class CatClusterer has six private data members, which are illustrated in Figure 2-b. For most developers, including me, having a diagram of the key data structures is essential when writing machine learning code. Class member rnd is used when generating candidate sets of initial tuples to be assigned to clusters, and when iterating through the remaining tuples in a random order.

The class exposes just two public methods: a constructor, and the clustering method. Helper method ClusterOnce performs one pass of the GACUC algorithm, returning the clustering found and the associated CU as an out-parameter. Method Cluster calls ClusterOnce numRestart times and returns the best clustering and CU found.

Helper methods MakeDataMatrix and Allocate are called by the class constructor. Method MakeDataMatrix accepts the matrix of raw string data to be clustered and returns the equivalent zero-based integer encoded matrix. An important design alternative is to preprocess the raw data and save the integer representation as a text file. Method Allocate allocates memory for the key data structures and is just a convenience to keep the constructor code tidy.

Method ClusterOnce, which does most of the work, calls helper methods GetGoodIndices, Assign, Unassign, Shuffle, and MaxIndex. Method GetGoodIndices generates initial data tuples that are different from each other. Assign updates all data structures to assign a tuple to a cluster. Unassign reverses the action of Assign. Method Shuffle is used to present data tuples in random order. Method MaxIndex is used to find the best proposed cluster assignment.

Private method Reservoir is a sub-helper called by helper method GetGoodIndices. Method Reservoir uses a mini-algorithm called reservoir sampling to find n distinct array indices. The CatClusterer class constructor is short:

public CatClusterer(int numClusters, string[][] rawData)

{

  this.numClusters = numClusters;

  MakeDataMatrix(rawData);

  Allocate();

}

A recurring theme when designing machine learning code is the decision of whether to pass the source data to the constructor or to the primary public method. Here, the data is passed to the constructor so that helper MakeDataMatrix can create the internal integer-form dataAsInts matrix.

The Cluster Method

Method Cluster is presented in Listing 2-c. Notice that the method does not accept a parameter representing the data to be clustered; the data is assumed to be available as a class member.

Listing 2-c: The Cluster Method

Method Cluster is essentially a wrapper around method ClusterOnce. Notice that the randomization seed value passed to method ClusterOnce is the value of current iteration variable, start. This trick is a common design pattern when using a restart algorithm so that the worker method does not return the same result in each iteration.

The definition of method ClusterOnce begins with:

private int[] ClusterOnce(int seed, out double catUtility)

{

  this.rnd = new Random(seed);

  Initialize();

. . .

Helper method Initialize performs three tasks. First, the values in the clustering array are all set to -1. This allows the algorithm to know whether a data tuple has been assigned to a cluster or not. Second, the values in clusterCounts are set to 0 to reset the array, which holds counts from any previous call to ClusterOnce. Third, the values in data structure valueCounts are set to 0.

Next, method ClusterOnce selects the first tuples and assigns them to clusters:

int numTrials = dataAsInts.Length;

int[] goodIndexes = GetGoodIndices(numTrials);

for (int k = 0; k < numClusters; ++k)

  Assign(goodIndexes[k], k);

Method GetGoodIndices returns numClusters data indices where the data tuples are different from each other. As explained earlier, it's usually not possible to examine all possible candidate sets of initial tuples, so numTrials of sets are examined. After these good indices (the data tuples are different) are found, their associated data tuples are assigned to clusters.

A short example will help clarify. For the demo data, with seven data tuples and number of clusters set to three, method GetGoodIndices might return { 6, 0, 1 }. These are the indices of three data items that are very different from each other, as defined by Hamming distance:

[6]  Red      Large    False
[0]  Blue     Small    False
[1]  Green    Medium   True

These three tuples, 6, 0, and 1, are assigned to clusters 0, 1, and 2, respectively. The resulting clustering data member would then be:

 1    2   -1   -1   -1   -1    0     (cluster ID)
[0]  [1]  [2]  [3]  [4]  [5]  [6]    (tuple index)

Next, the order of the data tuples is scrambled so that they will be presented in a random order:

int numRows = dataAsInts.Length;

int[] rndSequence = new int[numRows];

for (int i = 0; i < numRows; ++i)

  rndSequence[i] = i;

Shuffle(rndSequence);

Helper method Shuffle uses the Fisher-Yates algorithm to shuffle the data tuple indices. Use of the Fisher-Yates shuffle is very common in machine learning code.

At this point, the clustering algorithm walks through each tuple. If the current tuple has not been assigned to a cluster (the value in clustering will be -1 if unassigned), each possible value of cluster ID is examined, and the one cluster ID that gave the best clustering (the largest value of CU) is associated with the current tuple:

for (int t = 0; t < numRows; ++t)  // walk through each tuple

{

  int idx = rndSequence[t]; // index of data tuple to process

  if (clustering[idx] != -1) continue;  // already clustered

  double[] candidateCU = new double[numClusters];

  for (int k = 0; k < numClusters; ++k) // each possible cluster

  {

    Assign(idx, k); // tentative cluster assignment

    candidateCU[k] = CategoryUtility(); // compute and save the CU

    Unassign(idx, k); // undo tentative assignment

  }

  int bestK = MaxIndex(candidateCU);  // greedy. index is a cluster ID

  Assign(idx, bestK); // now we know which cluster gave the best CU

} // each tuple

At this point, all data tuples have been assigned to a cluster. Method ClusterOnce computes the final category utility and returns the clustering as an explicit return value, and the CU as an out-parameter:

. . .

  catUtility = CategoryUtility();

  int[] result = new int[numRows];

  Array.Copy(this.clustering, result, numRows);

  return result;

}

The CategoryUtility Method

The heart of the GACUC categorical data clustering algorithm is the method that computes category utility for a given clustering of data. Method CategoryUtility is relatively simple because it uses the precomputed counts stored in data structures valueCounts and clusterCounts.

The definition begins by computing the P(C_k) terms, the probabilities of each cluster:

private double CategoryUtility() // called by ClusterOnce

{

  int numTuplesAssigned = clusterCounts[clusterCounts.Length - 1];

  double[] clusterProbs = new double[this.numClusters];

  for (int k = 0; k < numClusters; ++k)

    clusterProbs[k] = (clusterCounts[k] * 1.0) / numTuplesAssigned;

. . .

Next, the single unconditional term (the sum of the unconditional probabilities) is computed:

double unconditional = 0.0;

for (int i = 0; i < valueCounts.Length; ++i)

{

  for (int j = 0; j < valueCounts[i].Length; ++j)

  {

    int sum = valueCounts[i][j][numClusters]; // last cell holds sum

    double p = (sum * 1.0) / numTuplesAssigned;

    unconditional += (p * p);

  }

}

Next, the numCluster conditional terms (the sums of conditional probabilities) are computed:

double[] conditionals = new double[numClusters];

for (int k = 0; k < numClusters; ++k)

{

  for (int i = 0; i < valueCounts.Length; ++i) // each att

  {

    for (int j = 0; j < valueCounts[i].Length; ++j) // each value

    {

      double p = (valueCounts[i][j][k] * 1.0) / clusterCounts[k];

      conditionals[k] += (p * p);

    }

  }

}

With the pieces of the puzzle computed, method CategoryUtility combines them according to the mathematical definition of category utility:

. . .
  double summation = 0.0;

  for (int k = 0; k < numClusters; ++k)

    summation += clusterProbs[k] * (conditionals[k] - unconditional);

  return summation / numClusters;

}

Method CategoryUtility is an internal method in the sense that it assumes all needed counts are available. You might want to consider writing a standalone public-scope version that creates and initializes local versions of valueCounts and clusterCounts, scans the clustering array and uses the dataAsInts matrix to populate the counts data structures, and then uses the counts to compute CU.

Clustering Initialization

The clustering initialization process is the primary customization point for the GACUC categorical data clustering algorithm. After initialization, GACUC clustering is deterministic, so the clustering result depends entirely on initialization. Initialization is implemented in method GetGoodIndices.

The method's definition begins:

private int[] GetGoodIndices(int numTrials)

{

  int numRows = dataAsInts.Length;

  int numCols = dataAsInts[0].Length;

  int[] result = new int[numClusters];

. . .

The goal is to find the indices of data tuples that are different from each other. Because it is not possible in most scenarios to examine all possible sets of candidate data tuples, parameter numTrials holds the number of times to examine randomly selected sets.

Even though not all possible sets of initial tuples can be examined, in general it is possible to compare all possible pairs of tuples within a set of candidates:

int largestDiff = -1;

for (int trial = 0; trial < numTrials; ++trial)

{

  int[] candidates = Reservoir(numClusters, numRows);

  int numDifferences = 0; // for these candidates

  for (int i = 0; i < candidates.Length - 1; ++i) // all possible pairs

  {

    for (int j = i + 1; j < candidates.Length; ++j)

    {

      int aRow = candidates[i];

      int bRow = candidates[j];

      for (int col = 0; col < numCols; ++col)

        if (dataAsInts[aRow][col] != dataAsInts[bRow][col])

          ++numDifferences;

    } // j

  } // i

. . .

This idea may be a bit confusing. Suppose the source data to cluster has 500 data items and the number of clusters is set to 3. There are Choose(500, 3) = 20,708,500 possible candidate sets of the initial three tuples, which is a lot. Suppose each data tuple has four attributes. To compare all possible pairs of any set of three tuples, there are Choose(3, 2) * 4 = 12 comparisons required, which is quite feasible.

In situations where the number of clusters is very large and the number of attributes is also large, you can modify GetGoodIndices to examine only adjacent pairs of the candidate tuples. The program listing at the end of this chapter provides example code for this.

The second initialization option is to use an alternative to the Hamming distance to measure the difference between two data tuples. Options you may wish to explore include metrics called cosine similarity, Goodall similarity, and Smirnov similarity.

Method GetGoodIndices concludes by tracking whether the current number of value differences is greater than the best (largest) found so far, and if so, saving the candidate set of tuple indices:

. . .
    if (numDifferences > largestDiff)

    {

      largestDiff = numDifferences;

      Array.Copy(candidates, result, numClusters);

    }

  } // trial

  return result;

}

Reservoir Sampling

Method GetGoodIndices calls a helper method named Reservoir. This utility method returns n random, distinct values from 0 to r - 1, which corresponds to n distinct array indices. Returning n random, distinct array indices is a very common machine learning task, and one that is surprisingly interesting.

For the demo program, with seven data tuples with indices 0 through 6 (so r = 7), and the number of clusters set to three (so n = 3), method GetGoodIndices must generate three distinct values from 0 through 6. There are three common ways to generate n random distinct array indices: brute force, shuffle-select, and reservoir sampling.

In pseudo-code, the brute force technique to generate n random integers between 0 and r - 1 is:

loop t times
  select n random integers between [0, r-1]
  if all n integers are different
    return the n integers
  end if
  // try again
end loop
return failure

The problem with the brute force approach is that there is no guarantee that you'll ever get n different values. However, brute force is very effective when the number of integers to generate (n) is very, very small compared to the range (r). For example, if the goal is to select n = 3 integers between 0 and 9999, the chances of getting a duplicate value among three random values is small.

In pseudo-code, the shuffle-select technique is:

create a scratch array of sequential integers from 0 through r-1
shuffle the values in the array (using Fisher-Yates)
select and return the first n values in the shuffled array

The problem with the shuffle-select approach is that it uses extra memory for the scratch array. However, shuffle-select is simple and effective when n is small (say, less than 1,000).

The demo program uses a very clever algorithm called reservoir sampling. In pseudo-code:

create a small result array of sequential integers from 0 through n-1
loop for t := n to r-1
  generate a random integer j between [0, t]
  if j < n
  set result[j] := t
end loop
return result

Reservoir sampling is not at all obvious, and is a rare example where the actual code is probably easier to understand than pseudo-code. The code for method Reservoir is:

private int[] Reservoir(int n, int range)

{

  // select n random indices between [0, range)

  int[] result = new int[n];

  for (int i = 0; i < n; ++i)

    result[i] = i;

  for (int t = n; t < range; ++t)

  {

    int j = rnd.Next(0, t + 1);

    if (j < n)

      result[j] = t;

  }

  return result;

}

Suppose the goal is to generate n = 3 random distinct integers between 0 and 6, inclusive. The result array is initialized to { 0, 1, 2 }. The first time through the algorithm's loop, t = 3. A random j is generated between 0 and 3 inclusive. Let’s suppose it is j = 2. Because (j = 2) < (n = 3), result[j = 2] is set to t = 3, so the result array is now { 0, 1, 3 }.

The second time through the loop, t = 4. Suppose generated j = 0. Because (j = 0) < (n = 3), result[j = 0] is set to t = 4 and result is now { 4, 1, 3 }.

The third time through the loop, t = 5. Suppose generated j = 4. Because (j = 4) is not less than (n = 3), result is not changed and remains { 4, 1, 3 }.

The fourth time through the loop, t = 6. Suppose generated j = 1. Because (j = 1) < (n = 3), result[j = 1] is set to 6 and result is now  { 4, 6, 3 }. The t-loop terminates and result is returned.

Clustering Mixed Data

The GACUC clustering algorithm is intended for categorical data items, but it can also be used to cluster data that contains a mixture of numeric and categorical data. The idea is to first convert numeric data into categorical data. For example, suppose the data items to be clustered represent people, and each item has attributes (sex, age, job). For example, the first two data items might be:

male, 28.0, engineer
female, 52.0, accountant

If you convert the raw age data so that ages 0 through 21 are low, ages 22 through 45 are medium, and ages 46 through 99 are high, the data items become:

male, medium, engineer
female, high, accountant

Now the data is all categorical and the GACUC algorithm can be used. Converting numeric data to categorical data is called discretizing the data, or binning the data.

With this example data, the GACUC algorithm does not take into account the fact that category high is closer to category medium than to category low. An unexplored option is to modify the GACUC algorithm to use categorical data closeness information.

Chapter 2 Complete Demo Program Source Code