CHAPTER 5
B-tree
Overview
A B-tree is a sorted, balanced tree structure. B-trees are typically used to access data stored on slow-access mediums such as tape drives and disks. The tree hierarchy makes it possible to store the data in a manner that is possible to search efficiently while only loading the necessary portions of the tree from the storage media into main memory.
This chapter will not address the issues of offline data storage, but will instead focus on an entirely in-memory data structure. Once you understand the concepts of the B-tree, they can be applied to loading data from a disk, but that is an exercise you can pursue on your own.
B-tree Structure
The easiest way to learn about the B-tree structure might be to look at a B-tree and discuss the ways that it differs from the tree structure we are already familiar with: the binary search tree. The following is an example of a B-tree:
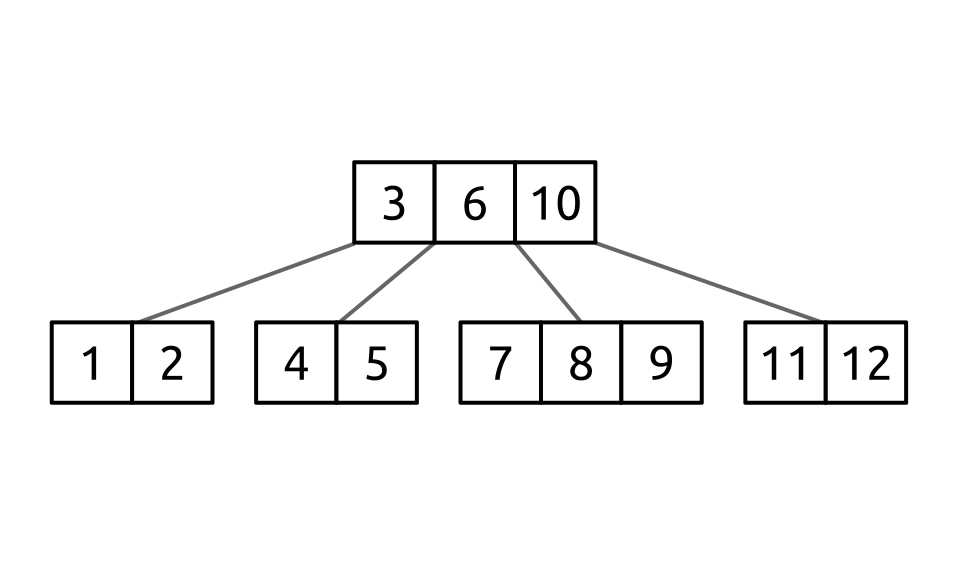
Figure 45: An example B-tree
To be clear, this is a B-tree with a root node containing the values [3, 6, 10], and four child nodes.
I want to emphasize that point: this tree contains five nodes and 12 values. While a binary search tree contains a single value per node, a B-tree can, and very frequently will, have more than one value per node.
You will notice that the ordering of the values in the tree is consistent with what we have seen with binary search trees. Smaller values are on the left and larger (or equivalent) values are on the right. This holds true both within the tree structure (the child nodes) and also for the ordering of values within the nodes.
In this example, the root node has three values and four children. This pattern of n values and n + 1 children is an immutable trait of a B-tree. Whether a node contains one or a thousand values, there will always be one more child than values. Take a moment to consider why this is true.
When navigating the tree, we start at the root node. The first value in the node is 3. Following the “smaller values on the left” rule, we need to have a node to the left to traverse down to (unless the node is a leaf node, in which case it has no children). Likewise, the value 3 needs to have a child to its right for the values greater than 3 (and less than its neighbor value, 6).
Notice that the right child of the value 3 is also the left child of the value 6. Similarly, the right child of the value 6 is the left child of the value 10. And finally the last value, 10, has a right child.
Minimal Degree
A critical and often confusing concept in a B-tree is the minimal degree. Also called the minimization factor, degree, order, and probably many other things, the key concept is the same.
The minimal degree is the minimum number of children that every node, except for the root node (which can have fewer, but not more), must have. Throughout this chapter I will refer to the minimal degree by the variable T.
More formally, each non-root node in the B-tree will contain at least T children and a maximum of 2 × T children. There are two important facts we can derive from this:
- Every non-root node will have at least T - 1 values.
- Every non-root node will have at most 2 × T - 1 values.
A node that has T - 1 values is at its minimal degree and cannot have a value removed from it. A node that has 2 × T - 1 is at its maximal degree and cannot have another value added to it. A node in this state is said to be “full.”
Tree Height
The B-tree structure enforces the rule that every leaf node in the tree will be at the same depth and each leaf node will contain data.
The tree we saw in Figure 45 had four leaf nodes all of which were at the same depth of 2. Two examples of invalid B-trees follow.
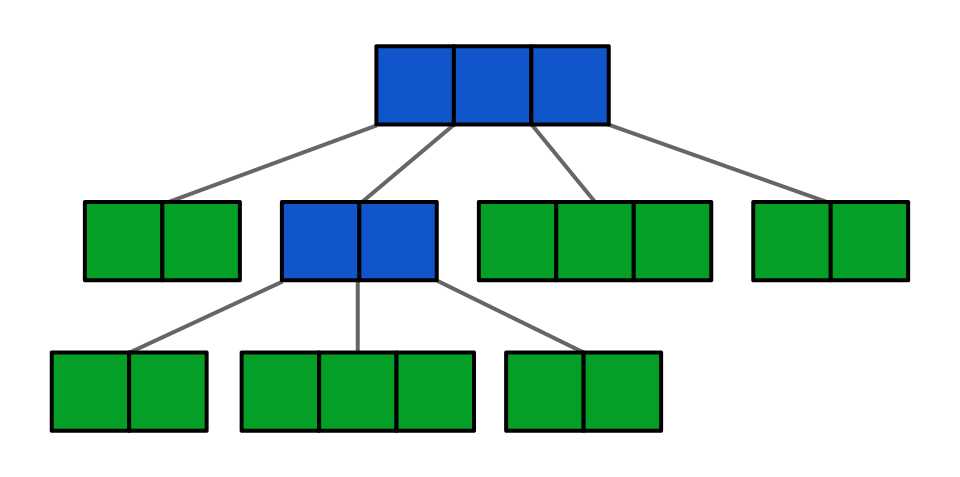
Figure 46: An invalid B-tree. The leaf nodes (green) are not all on the same level
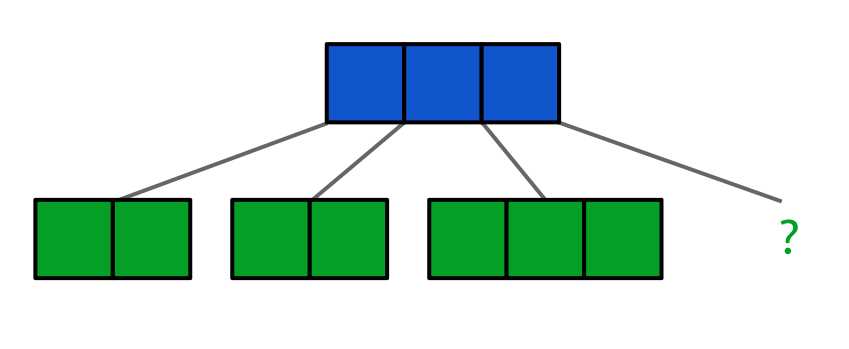
Figure 47: An invalid B-tree. The leaf nodes (green) are at the same height but one is empty or missing
Searching the Tree
Because of its ordered structure, searching a B-tree is similar to searching a binary search tree. The algorithm for searching for a value in the tree is pretty simple. The algorithm recursively processes each node, starting at the root, using the following algorithm:
bool search(node, valueToFind) foreach value in node if valueToFind == value return true if valueToFind < value search(<left child>, valueToFind) end return search(<last child>, valueToFind) end |
To see how it works, let’s work through a few scenarios searching the tree in the following figure:
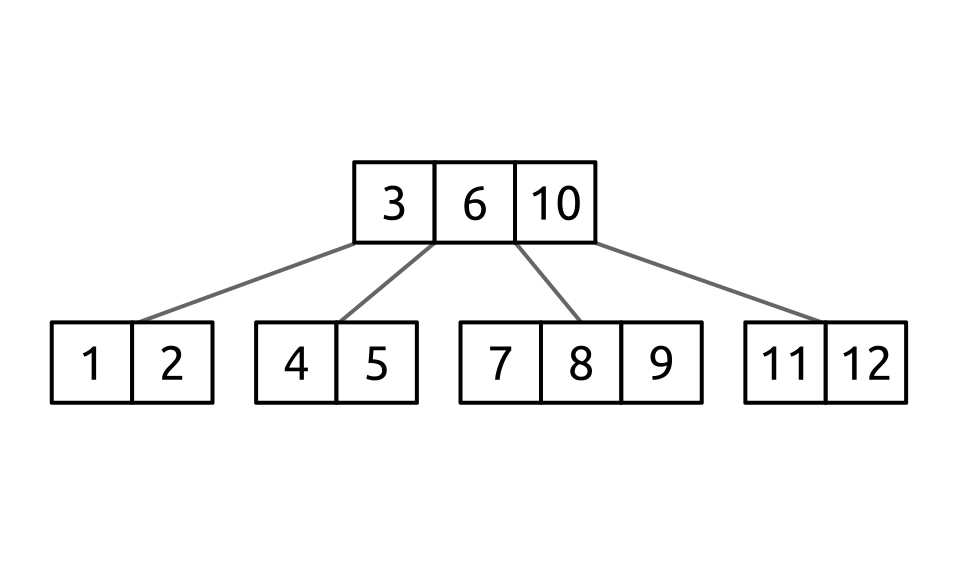
Figure 48: B-tree for searching
Searching for the value 3 is trivial. The search starts at the root node and the first value in the node (3) is compared against the value being sought (3) and the value is found.
Searching for 6 is similar. The 3 in the root node is compared with 6. Since 6 is larger than 3, the search moves to the next value in the node. The next value (6) is compared with the value being sought (6), and the value is found.
Searching for 2 is a little more complex. First, the value 2 is compared against the 3 in the root node. Since 2 is less than 3, the child to the left of 3 is searched. The first value in the child containing [1, 2] is searched. Since 1 is less than 2, the next value is checked. The value 2 matches the value being sought, so the value is found.
Searching for 15 starts by comparing against the 3, 6, and 10. Since they are all smaller than 15, the last child of the root node is searched. The process repeats comparing against the values 11 and 12. Since both are smaller, the last child node of the current node would be checked; however, the node [11, 12] is a leaf node so the value is not found.
It should be clear that the search algorithm is basically the same as the binary search tree algorithm with the distinction being that each node may have more than one value to compare against.
Putting It Together
With the understanding of tree height, minimal degree, and how to search the tree, let’s take a few moments to consider how efficient this structure is.
Imagine a tree with a minimal factor of 501. This tree will have at least 500 values in each non-root node (with a maximum of 1000). If the root node contains 500 values, and each of its 501 children contained 500 values, the first two levels alone would contain 500 × 502, or 251,000, values.
To find a specific value we would start at the root node and perform at most 500 comparisons. Along the way we would either find the value we want or determine which node to check next. At that next node we would again perform at most 500 comparisons or determine the node was not there. This means we would perform at most 1000 comparisons in a tree with 251,000 values.
But it could be even better!
Since each node contains a sorted array of values, we could use a binary search instead of a linear search. We can now perform only 9 comparisons per node, and in only 18 comparisons—in the worst case—determine whether or not the value exists in a tree of 251,000 values.
Balancing Operations
Like an AVL tree, when an operation that changes the tree structure occurs, a B-tree may need to be balanced to ensure that it implements the structural rules. While conceptually similar, the actual operations are quite different from how an AVL works.
In this section, we are going to look at several types of balancing operations and discuss what purpose they serve.
Pushing Down
Pushing a value down is a process in which two child nodes are merged together with a value from the parent pushed down into the resulting node as the median value. Let’s take a look at what this means. We start with the following tree:
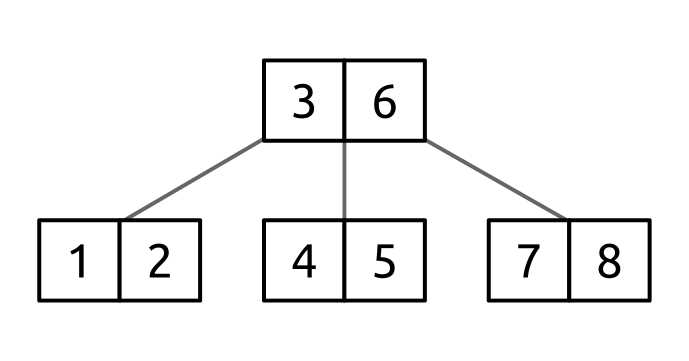
Figure 49: B-tree for pushing down
Say this is a tree with degree 3. This means that each node must have between 2 and 5 values (with the exception of the root node). With that understanding, how would we delete the value 2 from this tree? If we simply removed the 2 from the leaf node, the child node [1, 2] would be left with only a single value in it. Since that would violate the B-tree structural rules, it is not an acceptable solution.
What we need is for the value 2 to exist within a node that has at least T values in it that also abides by the other B-tree structural rules. To do this, we are going to create a new node by doing the following:
- Allocate a new node.
- Put the values [1, 2] into the new node.
- Put the value [3] into the new node.
- Put the values [4, 5] into the new node.
- Discard the existing nodes [1, 2] and [4, 5].
- Remove the value [3] from the parent node.
- Link the new node where [4, 5] was previously linked.
This results in a tree that looks like the following:
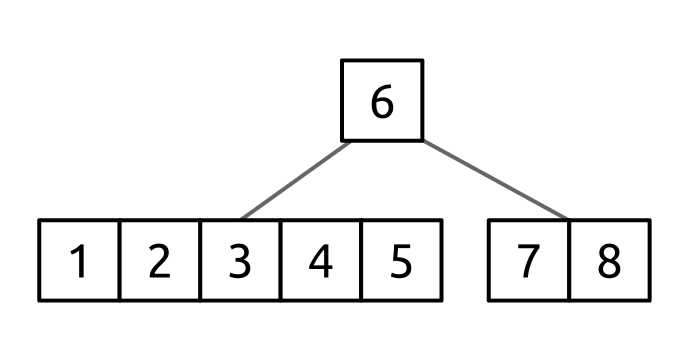
Figure 50: Pushed down B-tree
We now have a node with 2 × T - 1 values in it, which is more than enough to delete the value 2.
Key points:
- Push down merges two adjacent children.
- Each of those children have T - 1 values.
- The parent value is added as the median value.
- The resulting node has 2 × T - 1 values.
Rotating Values
Value rotation is very similar to push down and is done for the same reasons, just in a slightly different situation.
Consider the following tree:
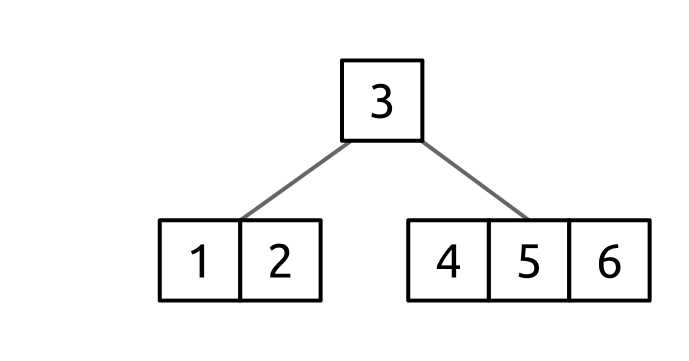
Figure 51: B-tree for rotating
Like we did with push down, let’s look at how we would remove the value 2 from the tree when the node that contains 2 has only T - 1 values.
The key to resolving this issue is that [1, 2]’s sibling node, [4, 5 ,6], has more than T - 1 values and therefore can have a value taken from it without violating the structural rules. This is done by rotating the value we want to take through the parent as shown below.
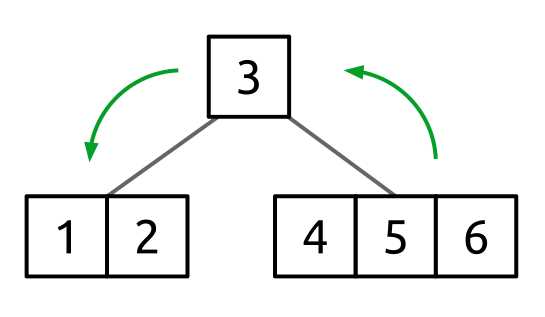
Figure 52: B-tree before rotation
The value we are going to rotate (4) is going to rotate to the parent node, and the parent value (3) is going to rotate to the child node, giving a resulting tree of:
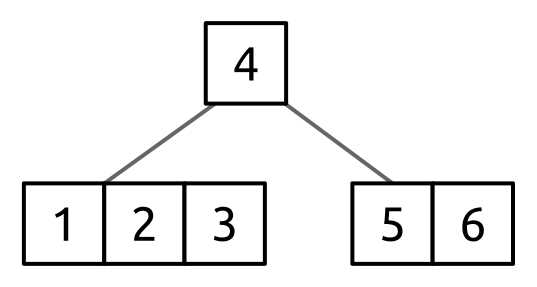
Figure 53: B-tree after rotation
With this rotation done, the value 2 can now be deleted from the leaf node.
The specific steps that occurred here are:
- Add the parent value to the end of the left child’s values.
- This is adds the value 3 to the [1, 2] node, making the node [1, 2, 3].
- Copy the first value of the right sibling’s values (4) to the parent (where 3 was).
- At this point, 4 exists in both the root node [4] and still in [4, 5, 6].
- If the [4,5,6] node is not a leaf node, move the left child of 4 to be the right child of 3 in [1, 2, 3].
- This works because everything that was left of 4 in [4, 5, 6] is, by definition, less than 4 but greater than 3. Now that 4 is the root, we know that all the values on that sub-tree belong to its left. Similarly, we know that all the values in that sub-tree are greater than 3 so they belong to its right.
Be aware that the steps we just followed were for rotating a node from the right to the left. The opposite process of rotating a node from the left to the right can be done by simply reversing the direction of the operations described previously.
Splitting Nodes
Splitting a node is basically the opposite of a push down. Instead of merging two nodes together with a median value provided by the parent, we are splitting a node in half and pulling the median value up into the parent.
For example, given the following tree:
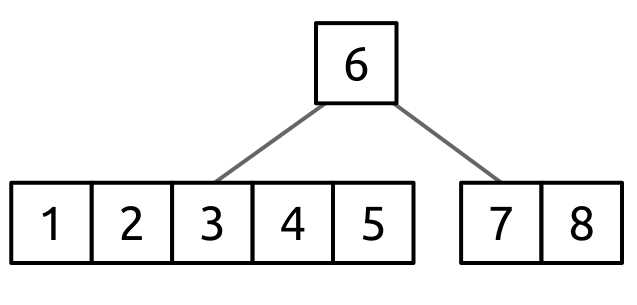
Figure 54: B-tree for splitting
We want to split the node [1, 2, 3, 4, 5] and move its median value, 3, to the parent, creating the new root [3, 6]. This would result in the following tree:
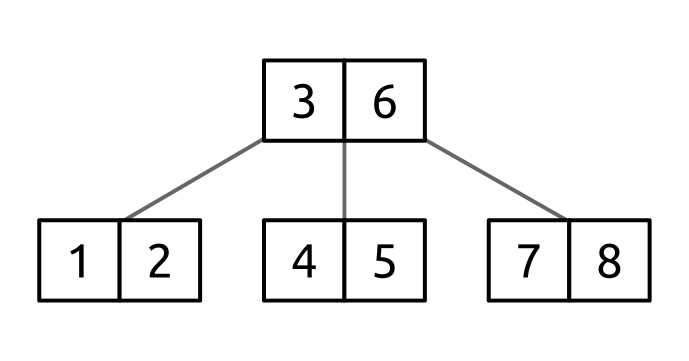
Figure 55: B-tree after splitting the left child node
The steps here are:
- Pick the median value from the node [1, 2, 3, 4, 5].
- Create the new left child [1, 2].
- Create the new right child [4, 5].
- Move the value 3 to the front of the root, creating [3, 6].
- Link the new nodes [1, 2] and [4, 5] as the left and right children of the parent value [3].
When would we do this?
In our example, adding another value to the node [1, 2, 3, 4, 5] would cause the node to have more than 2T - 1 values, which violates the B-tree structural rules. Since [1, 2, 3, 4, 5] is a leaf node, we cannot simply create a new child of [1, 2, 3, 4, 5] because that would invalidate the rule that all leaf nodes must be at the same height.
We can use node splitting to address this by moving a value from the child to the parent, ensuring that both the new left and right children have sufficient space for a new value to be added without invalidating the structural rules.
Adding Values
Adding a value into a B-tree is done using a relatively simple algorithm that makes use of the balancing operations described in previous sections. The insertion process starts at the root node where the following logic occurs:
BTree::Add(value) IF root.Values.Count == (2 × T – 1) THEN root = SplitRootNode(root) END AddToNonFullNode(root, value) END |
There are two paths here, and which is taken depends on whether the root node is full at the time the Add is performed. Let’s take a look at what happens in this scenario.
We start with a tree that has a minimum factor of 3. This means the root node can have 0 (empty) to 5 (full) values in it. In this scenario, the entire tree has 5 values in it and they all exist in the root node. The starting tree is:
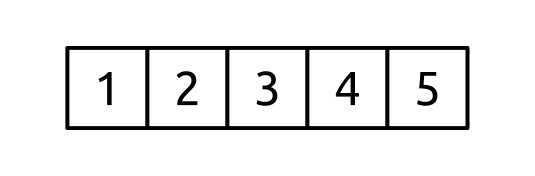
Figure 56: B-tree with all its values in the root node
At this point, we want to add the value 6 to the tree. Adding the value to the root node would give it 2T values, which is more than it can hold. To deal with this, we need to use the node splitting algorithm.
To do this, the median value of the root node, 3, is pulled up into a new root node and the adjacent values [1, 2] and [4, 5] become child nodes of the root. When this is complete, the tree looks like the following:
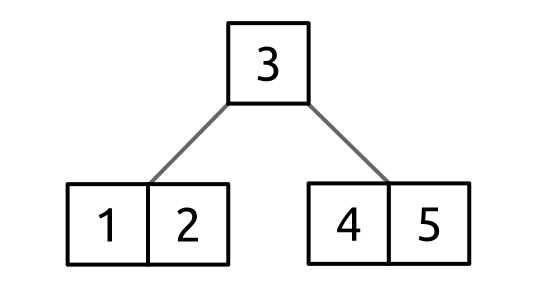
Figure 57: B-tree after splitting the root node
An interesting and very important point to understand is that this process of splitting the root node is the only way that the height of the tree grows.
Now that the root node is not full (or if the node was not full when Add was called), the non-full insertion algorithm can be performed.
This algorithm simply searches for the appropriate leaf node to add the value to and splits any full node encountered as it traverses down the tree. A simplified version of this algorithm follows:
BTree::AddToNonFullNode(node, value) IF node.Leaf THEN AddValueAtAppropriateIndex(node, value) ELSE child = FindAppropriateChildToInsert(node, value) IF child.Values.Count = (2 × T – 1) THEN SplitChildNode(node, child) END AddToNonFullNode(child, value) END END |
There are two key points you need to understand about this algorithm:
- Values are only ever added to leaf nodes.
- The algorithm never traverses into a full node; it always splits full nodes before going into them. This is critical because it means the leaf node the value is inserted into cannot be full.
Removing Values
Much like a binary search tree or AVL tree, removing a value from a B-tree is more complex than adding a value. In the case of a B-tree, there are three potential states that need to be dealt with:
- The value to remove is in a leaf node.
- In this case, we can simply remove the value.
- The value is in an internal (non-leaf) node.
- Push the value to be removed down one level (toward a leaf node). Use the various balancing algorithms to ensure the tree stays structurally valid as the value is pushed down.
- Traverse into the child node where the value was pushed and repeat from step 1.
- The value is not in the current internal node.
- Find the child node where the value would be if it is in the tree.
- Ensure the child node has at least T values in it.
- Use the node rotation or merge algorithm on the child to ensure that it has T nodes before traversing to it.
- Traverse into the child node and repeat from step 1.
At a really high level, what is happening is we are walking down the tree, from the root to the appropriate leaf node, and along the way making sure of the following:
- If we have found the value to remove, we push it down toward a leaf node.
- If we have not, make sure the child node has T children before going to it.
The reason we do #1 is because we can only remove (and add) items in leaf nodes. This is not just because doing that is “easier,” but because doing it is mandatory. Each node has n values and n + 1 children. In a non-leaf node, each of those children references an entire subtree of nodes. If we removed a value from an internal node, we would have n - 1 values and n + 1 children. How would we manage that orphaned child tree?
The only way we can safely remove (or add) an item from the tree is in a leaf node. This is because leaf nodes are the only ones that do not have this problem of managing children (because they have none).
And why do we do #2? We do it because if we don’t, then we can’t do #1. #1 says when we enter the internal node we will have n values, and when we are done we will have n - 1 values. If we started the process with T - 1 values (the minimum a node can contain), we would not be able to remove the node without violating the structural rules of the B-tree. So to make sure we can safely traverse to the child, we first ensure that the node has at least T values. This way if we push a value down, the node will still have at least T - 1 values and therefore still be valid.
B-tree Node
The B-tree has an internal node class that manages the values, pointers to the children, and a Boolean indicator for whether the node is a leaf node.
The BTreeNode class in the next example is pretty extensively commented and the concepts used were detailed previously in this chapter. Because of that, large sections of code will stand on their own with little additional commentary.
BTreeNode Class
The BTreeNode class manages the operations to add and remove values from leaf nodes, push down a value into a child node, and node splitting. Additionally, it provides some helper methods and properties used by the push down and splitting algorithms.
There is also a pair of validation methods used by the constructor and during operations that change the tree structure. They serve as a sanity check that the BTree class is not providing inappropriate parameters to the constructor and that the tree has not moved from a valid to invalid state.
internal class BTreeNode<T> where T : IComparable<T> { private readonly List<T> _values; private readonly List<BTreeNode<T>> _children; internal BTreeNode(BTreeNode<T> parent, bool leaf, int minimumDegree, T[] values, BTreeNode<T>[] children) { ValidatePotentialState(parent, leaf, minimumDegree, values, children); Parent = parent; Leaf = leaf; MinimumDegree = minimumDegree; _values = new List<T>(values); _children = new List<BTreeNode<T>>(children); } /// <summary> /// Returns true if the node has (2 * T - 1) nodes, false otherwise. /// </summary> internal bool Full { get; } /// <summary> /// True if the node is a leaf node, false otherwise. /// </summary> internal bool Leaf { get; private set; } /// <summary> /// The node's values. /// </summary> internal IList<T> Values { get; } /// <summary> /// The node's children. /// </summary> internal IList<BTreeNode<T>> Children { get; } /// <summary> /// The minimum degree of the node is the minimum degree of the tree. /// If the minimum degree is T then the node must have at least T - 1 /// values, but no more than 2 * T - 1. /// </summary> internal int MinimumDegree { get; private set; } /// <summary> /// The parent of the current node (or null if the root node). /// </summary> internal BTreeNode<T> Parent { get; set; } /// <summary> /// Splits a full child node, pulling the split value into the current node. /// </summary> /// <param name="indexOfChildToSplit">The child to split.</param> internal void SplitFullChild(int indexOfChildToSplit); /// <summary> /// Splits the full root node into a new root and two children. /// </summary> /// <returns>The new root node.</returns> internal BTreeNode<T> SplitFullRootNode(); /// <summary> /// Insert the specified value into the non-full leaf node. /// </summary> internal void InsertKeyToLeafNode(T value); /// <summary> /// Removes the specified value from the leaf node if it exists. /// </summary> /// <param name="value">The value to remove.</param> /// <returns>True if a value was removed, false otherwise.</returns> internal bool DeleteKeyFromLeafNode(T value); /// <summary> /// Replaces the value at the specified index with the new value. /// </summary> internal void ReplaceValue(int valueIndex, T newValue); // [3 6] // [1 2] [4 5] [7 8] // becomes // [6] // [1 2 3 4 5] [7 8] internal BTreeNode<T> PushDown(int valueIndex); /// <summary> /// Adds the specified value to the front of the values and, if non-null, /// adds the specified value to the children. /// </summary> internal void AddFront(T newValue, BTreeNode<T> bTreeNode); /// <summary> /// Adds the specified value to the node and, if the specified node is non-null, /// adds the node to the children. /// </summary> internal void AddEnd(T valueToPushDown, BTreeNode<T> bTreeNode); /// <summary> /// Removes the first value and child (if applicable). /// </summary> internal void RemoveFirst(); /// <summary> /// Removes the last value and child (if applicable). /// </summary> internal void RemoveLast(); } |
Adding, Removing, and Updating Values
This section shows the code for methods that manage adding and removing values from leaf nodes. Additionally, a method for updating a value within the node (called by the BTree class when moving values around) is shown.
/// <summary> /// Insert the specified value into the non-full leaf node. /// </summary> /// <param name="value">The value to insert.</param> internal void InsertKeyToLeafNode(T value) { // Leaf validation is done by caller. if (!Leaf) { throw new InvalidOperationException("Unable to insert into a non-leaf node"); } // Non-full validation done by caller. if (Full) { throw new InvalidOperationException("Unable to insert into a full node"); } // Find the index to insert at. int index = 0; while (index < Values.Count && value.CompareTo(Values[index]) > 0) { index++; } // Insert. _values.Insert(index, value); // Sanity check. ValidateValues(); } /// <summary> /// Removes the specified value from the leaf node if it exists. /// </summary> /// <param name="value">The value to remove.</param> /// <returns>True if a value is removed, false otherwise.</returns> internal bool DeleteKeyFromLeafNode(T value) { if (!Leaf) { throw new InvalidOperationException("Unable to leaf-delete from a non-leaf node"); } return _values.Remove(value); } /// <summary> /// Replaces the value at the specified index with the new value. /// </summary> /// <param name="valueIndex">The index of the value to replace.</param> /// <param name="newValue">The new value.</param> internal void ReplaceValue(int valueIndex, T newValue) { _values[valueIndex] = newValue; ValidateValues(); } |
Splitting Node
The algorithms for splitting a full child and for splitting the full root node are shown in the following code. These are very similar operations but have slightly different behaviors for the different scenarios.
/// <summary> /// Splits a full child node, pulling the split value into the current node. /// </summary> /// <param name="indexOfChildToSplit">The child to split.</param> internal void SplitFullChild(int indexOfChildToSplit) { // Splits a child node by pulling the middle node up from it // into the current (parent) node. // [3 9] // [1 2] [4 5 6 7 8] [10 11] // // Splitting [4 5 6 7 8] would pull 6 up to its parent. // // [3 6 9] // [1 2] [4 5] [7 8] [10 11] int medianIndex = Children[indexOfChildToSplit].Values.Count / 2; bool isChildLeaf = Children[indexOfChildToSplit].Leaf; // Get the value 6. T valueToPullUp = Children[indexOfChildToSplit].Values[medianIndex]; // Build node [4 5]. BTreeNode<T> newLeftSide = new BTreeNode<T>(this, isChildLeaf, MinimumDegree, Children[indexOfChildToSplit].Values.Take(medianIndex).ToArray(), Children[indexOfChildToSplit].Children.Take(medianIndex + 1).ToArray()); // Build node [7 8]. BTreeNode<T> newRightSide = new BTreeNode<T>(this, isChildLeaf, MinimumDegree, Children[indexOfChildToSplit].Values.Skip(medianIndex + 1).ToArray(), Children[indexOfChildToSplit].Children.Skip(medianIndex + 1).ToArray()); // Add 6 to [3 9], making [3 6 9]. _values.Insert(indexOfChildToSplit, valueToPullUp); // Sanity check. ValidateValues(); // Remove the child that pointed to the old node [4 5 6 7 8]. _children.RemoveAt(indexOfChildToSplit); // Add the child pointing to [4 5] and [7 8]. _children.InsertRange(indexOfChildToSplit, new[] { newLeftSide, newRightSide }); } /// <summary> /// Splits the full root node into a new root and two children. /// </summary> /// <returns>The new root node.</returns> internal BTreeNode<T> SplitFullRootNode() { // The root of the tree, and in fact the entire tree, is // // [1 2 3 4 5] // // So pull out 3 and split the left and right side: // // [3] // [1 2] [4 5] // Find the index of the value to pull up: 3. int medianIndex = Values.Count / 2; // Now get the 3. T rootValue = Values[medianIndex]; // Build the new root node (empty). BTreeNode<T> result = new BTreeNode<T>(Parent, false, MinimumDegree, new T[0], new BTreeNode<T>[0]); // Build the left node [1 2]. BTreeNode<T> newLeftSide = new BTreeNode<T>(result, Leaf, MinimumDegree, Values.Take(medianIndex).ToArray(), Children.Take(medianIndex + 1).ToArray()); // Build the right node [4 5]. BTreeNode<T> newRightSide = new BTreeNode<T>(result, Leaf, MinimumDegree, Values.Skip(medianIndex + 1).ToArray(), Children.Skip(medianIndex + 1).ToArray()); // Add the 3 to the root node. result._values.Add(rootValue); // Add the left child [1 2]. result._children.Add(newLeftSide); // Add the right child [4 5]. result._children.Add(newRightSide); return result; } |
Pushing Down
This code implements the push down algorithm documented previously.
// [3 6] // [1 2] [4 5] [7 8] // becomes // [6] // [1 2 3 4 5] [7 8] internal BTreeNode<T> PushDown(int valueIndex) { List<T> values = new List<T>(); // [1 2] -> [1 2] values.AddRange(Children[valueIndex].Values); // [3] -> [1 2 3] values.Add(Values[valueIndex]); // [4 5] -> [1 2 3 4 5] values.AddRange(Children[valueIndex + 1].Values); List<BTreeNode<T>> children = new List<BTreeNode<T>>(); children.AddRange(Children[valueIndex].Children); children.AddRange(Children[valueIndex + 1].Children); BTreeNode<T> newNode = new BTreeNode<T>(this, Children[valueIndex].Leaf, MinimumDegree, values.ToArray(), children.ToArray()); // [3 6] -> [6] _values.RemoveAt(valueIndex); // [c1 c2 c3] -> [c2 c3] _children.RemoveAt(valueIndex); // [c2 c3] -> [newNode c3] _children[valueIndex] = newNode; return newNode; } /// <summary> /// Adds the specified value to the node and, if the specified node is non-null, /// adds the node to the children. /// </summary> internal void AddEnd(T valueToPushDown, BTreeNode<T> bTreeNode) { _values.Add(valueToPushDown); ValidateValues(); if (bTreeNode != null) { _children.Add(bTreeNode); } } /// <summary> /// Removes the first value and child (if applicable). /// </summary> internal void RemoveFirst() { _values.RemoveAt(0); if (!Leaf) { _children.RemoveAt(0); } } /// <summary> /// Removes the last value and child (if applicable). /// </summary> internal void RemoveLast() { _values.RemoveAt(_values.Count - 1); if (!Leaf) { _children.RemoveAt(_children.Count - 1); } } /// <summary> /// Adds the specified value to the front of the values and, if non-null, /// adds the specified value to the children. /// </summary> internal void AddFront(T newValue, BTreeNode<T> bTreeNode) { _values.Insert(0, newValue); ValidateValues(); if (bTreeNode != null) { _children.Insert(0, bTreeNode); } } |
Validation
The following code performs basic validation for the constructor parameters and the tree state after a value is added or removed from the tree.
// Validates the constructor parameters. private static void ValidatePotentialState(BTreeNode<T> parent, bool leaf, int minimumDegree, T[] values, BTreeNode<T>[] children) { bool root = parent == null; if (values == null) { throw new ArgumentNullException("values"); } if (children == null) { throw new ArgumentNullException("children"); } if (minimumDegree < 2) { throw new ArgumentOutOfRangeException("minimumDegree", "The minimum degree must be greater than or equal to 2"); } if (values.Length == 0) { if (children.Length != 0) { throw new ArgumentException("An empty node cannot have children"); } } else { if (values.Length > (2 * minimumDegree - 1)) { throw new ArgumentException("There are too many values"); } if (!root) { if (values.Length < minimumDegree - 1) { throw new ArgumentException("Each non-root node must have at least degree - 1 children"); } } if (!leaf && !root) { if (values.Length + 1 != children.Length) { throw new ArgumentException("There should be one more child than values"); } } } } [Conditional("DEBUG")] private void ValidateValues() { if (_values.Count > 1) { for (int i = 1; i < _values.Count; i++) { Debug.Assert(_values[i - 1].CompareTo(_values[i]) < 0); } } } |
B-tree
The BTree class is what pulls together everything we’ve looked at in this chapter. As with BTreeNode, because the code is extensively commented and the core concepts are covered previously in this chapter, the code will basically stand on its own.
BTree Class
The BTree class implements the ICollection<T> interface and therefore provides the basic operations to add, remove, search, copy, count, clear, and enumerate (using an inorder traversal). Additionally, it has a reference to the root node (which will be null when the tree is empty), and a constant value that dictates the minimum degree of the tree (which in turn defines the minimum degree for every node).
public class BTree<T> : ICollection<T> where T : IComparable<T> { BTreeNode<T> root = null; const int MinimumDegree = 2; public void Add(T value); public bool Remove(T value); public bool Contains(T value); public void Clear(); public void CopyTo(T[] array, int arrayIndex); public int Count { get; private set; } public bool IsReadOnly { get; } public IEnumerator<T> GetEnumerator(); System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator(); } |
Add
Behavior | Adds the specified value to the tree. |
Performance | O(log n) |
This code implements the insertion algorithm previously described.
public void Add(T value) { if (root == null) { root = new BTreeNode<T>(null, true, MinimumDegree, new[] { value }, new BTreeNode<T>[] { }); } else { if (root.Full) { root = root.SplitFullRootNode(); } InsertNonFull(root, value); } Count++; } private void InsertNonFull(BTreeNode<T> node, T value) { if (node.Leaf) { node.InsertKeyToLeafNode(value); } else { int index = node.Values.Count - 1; while (index >= 0 && value.CompareTo(node.Values[index]) < 0) { index--; } index++; if (node.Children[index].Full) { node.SplitFullChild(index); if (value.CompareTo(node.Values[index]) > 0) { index++; } } InsertNonFull(node.Children[index], value); } } |
Remove
Behavior | Removes the first occurrence of the specified value from the tree. Returns true if a value was found and removed. Otherwise it returns false. |
Performance | O(log n) |
This code implements the remove algorithm previously described.
public bool Remove(T value) { bool removed = false; if (Count > 0) { removed = RemoveValue(root, value); if (removed) { Count--; if (Count == 0) { root = null; } else if (root.Values.Count == 0) { root = root.Children[0]; } } } return removed; } internal static bool RemoveValue(BTreeNode<T> node, T value) { if (node.Leaf) { // Deletion case 1... // By the time we are in a leaf node, we have either pushed down // values such that the leaf node has minimum degree children // and can therefore have one node removed, OR the root node is // also a leaf node and we can freely violate the minimum rule. return node.DeleteKeyFromLeafNode(value); } int valueIndex; if (TryGetIndexOf(node, value, out valueIndex)) { // Deletion case 2... // We have found the non-leaf node the value is in. Since we can only delete values // from a leaf node, we need to push the value to delete down into a child. // If the child that precedes the value to delete (the "left" child) has // at least the minimum degree of children... if (node.Children[valueIndex].Values.Count >= node.Children[valueIndex].MinimumDegree) { // [3 6 10] // [1 2] [4 5] [7 8 9] [11 12] // Deleting 10. // Find the largest value in the child node that contains smaller values // than what is being deleted (this is the value 9)... T valuePrime = FindPredecessor(node, valueIndex); // and REPLACE the value to delete with the next largest value (the one // we just found--swapping 9 and 10). node.ReplaceValue(valueIndex, valuePrime); // After the swap... // [3 6 9] // [1 2] [4 5] [7 8 9] [11 12] // notice that 9 is in the tree twice. This is not a typo. We are about // to delete it from the child we took it from. // Delete the value we moved up (9) from the child (this may in turn // push it down to subsequent children until it is in a leaf). return RemoveValue(node.Children[valueIndex], valuePrime); // Final tree: // [3 6 9] // [1 2] [4 5] [7 8 ] [11 12] } else { // If the left child did not have enough values to move one of its values up, // check whether the right child does. if (node.Children[valueIndex + 1].Values.Count >= node.Children[valueIndex + 1].MinimumDegree) { // See the previous algorithm and do the opposite... // [3 6 10] // [1 2] [4 5] [7 8 9] [11 12] // Deleting 6. // Successor = 7. T valuePrime = FindSuccessor(node, valueIndex); node.ReplaceValue(valueIndex, valuePrime); // After replacing 6 with 7, the tree is: // [3 7 10] // [1 2] [4 5] [7 8 9] [11 12] // Now remove 7 from the child. return RemoveValue(node.Children[valueIndex + 1], valuePrime); // Final tree: // [3 7 10] // [1 2] [4 5] [8 9] [11 12] } else { // If neither child has the minimum degree of children, it means they // both have (minimum degree - 1) children. Since a node can have // (2 * <minimum degree> - 1) children, we can safely merge the two nodes // into a single child. // // [3 6 9] // [1 2] [4 5] [7 8] [10 11] // // Deleting 6. // // [4 5] and [7 8] are merged into a single node with [6] pushed down //into it. // // [3 9] // [1 2] [4 5 6 7 8] [10 11] // BTreeNode<T> newChildNode = node.PushDown(valueIndex); // Now that we've pushed the value down a level, we can call remove // on the new child node [4 5 6 7 8]. return RemoveValue(newChildNode, value); } } } else { // Deletion case 3... // We are at an internal node which does not contain the value we want to delete. // First, find the child path that the value we want to delete would be in. // If it exists in the tree... int childIndex; FindPotentialPath(node, value, out valueIndex, out childIndex); // Now that we know where the value should be, we need to ensure that the node // we are going to has the minimum number of values necessary to delete from. if (node.Children[childIndex].Values.Count == node.Children[childIndex].MinimumDegree - 1) { // Since the node does not have enough values, what we want to do is borrow // a value from a sibling that has enough values to share. // Determine if the left or right sibling has the most children. int indexOfMaxSibling = GetIndexOfMaxSibling(childIndex, node); // If a sibling with values exists (maybe we're // at the root node and don't have one) // and that sibling has enough values... if (indexOfMaxSibling >= 0 && node.Children[indexOfMaxSibling].Values.Count >= node.Children[indexOfMaxSibling].MinimumDegree) { // Rotate the appropriate value from the sibling // through the parent and into the current node // so that we have enough values in the current // node to push a value down into the // child we are going to check next. // [3 7] // [1 2] [4 5 6] [8 9] // // The node we want to travel through is [1 2], but we // need another node in it. So we rotate the 4 // up to the root and push the 3 down into the [1 2] // node. // // [4 7] // [1 2 3] [5 6] [7 8] RotateAndPushDown(node, childIndex, indexOfMaxSibling); } else { // Merge (which may push the only node in the root down--so new root). BTreeNode<T> pushedDownNode = node.PushDown(valueIndex); // Now find the node we just pushed down. childIndex = 0; while (pushedDownNode != node.Children[childIndex]) { childIndex++; } } } return RemoveValue(node.Children[childIndex], value); } } internal static void RotateAndPushDown(BTreeNode<T> node, int childIndex, int indexOfMaxSibling) { int valueIndex; if (childIndex < indexOfMaxSibling) { valueIndex = childIndex; } else { valueIndex = childIndex - 1; } if (indexOfMaxSibling > childIndex) { // We are moving the leftmost key from the right sibling into the parent // and pushing the parent down into the child. // // [6 10] // [1] [7 8 9] [11] // // Deleting something less than 6. // // [7 10] // [1 6] [8 9] [11] // Grab the 7. T valueToMoveToX = node.Children[indexOfMaxSibling].Values.First(); // Get 7's left child if it has one (not a leaf). BTreeNode<T> childToMoveToNode = node.Children[indexOfMaxSibling].Leaf ? null : node.Children[indexOfMaxSibling].Children.First(); // Record the 6 (the push down value). T valueToMoveDown = node.Values[valueIndex]; // Move the 7 into the parent. node.ReplaceValue(valueIndex, valueToMoveToX); // Move the 6 into the child. node.Children[childIndex].AddEnd(valueToMoveDown, childToMoveToNode); // Remove the first value and child from the sibling now that they've been moved. node.Children[indexOfMaxSibling].RemoveFirst(); } else { // We are moving the rightmost key from the left sibling into the parent // and pushing the parent down into the child. // // [6 10] // [1] [7 8 9] [11] // // Deleting something greater than 10. // // [6 9] // [1] [7 8] [10, 11] // Grab the 9. T valueToMoveToX = node.Children[indexOfMaxSibling].Values.Last(); // Get 9's right child if it has one (not a leaf node). BTreeNode<T> childToMoveToNode = node.Children[indexOfMaxSibling].Leaf ? null : node.Children[indexOfMaxSibling].Children.Last(); // Record the 10 (the push down value). T valueToMoveDown = node.Values[valueIndex]; // Move the 9 into the parent. node.ReplaceValue(valueIndex, valueToMoveToX); // Move the 10 into the child. node.Children[childIndex].AddFront(valueToMoveDown, childToMoveToNode); // Remove the last value and child from the sibling now that they've been moved. node.Children[indexOfMaxSibling].RemoveLast(); } } internal static void FindPotentialPath(BTreeNode<T> node, T value, out int valueIndex, out int childIndex) { // We want to find out which child the value we are searching for (value) // would be in if the value were in the tree. childIndex = node.Children.Count - 1; valueIndex = node.Values.Count - 1; // Start at the rightmost child and value indexes and work // backward until we are at less than the value we want. while (valueIndex > 0) { int compare = value.CompareTo(node.Values[valueIndex]); if (compare > 0) { break; } childIndex--; valueIndex--; } // If we make it all the way to the last value... if (valueIndex == 0) { // If the value we are searching for is less than the first // value in the node, then the child is the 0 index child, // not the 1 index. if (value.CompareTo(node.Values[valueIndex]) < 0) { childIndex--; } } } // Returns the index (to the left or right) of the child node // that has the most values in it. // // Example // // [3 7] // [1 2] [4 5 6] [8 9] // // If we pass in the [3 7] node with index 0, the left child [1 2] // and right child [4 5 6] would be checked and the index 1 for child // node [4 5 6] would be returned. // // If we checked [3 7] with index 1, the left child [4 5 6] and the // right child [8 9] would be checked and the value 1 would be returned. private static int GetIndexOfMaxSibling(int index, BTreeNode<T> node) { int indexOfMaxSibling = -1; BTreeNode<T> leftSibling = null; if (index > 0) { leftSibling = node.Children[index - 1]; } BTreeNode<T> rightSibling = null; if (index + 1 < node.Children.Count) { rightSibling = node.Children[index + 1]; } if (leftSibling != null || rightSibling != null) { if (leftSibling != null && rightSibling != null) { indexOfMaxSibling = leftSibling.Values.Count > rightSibling.Values.Count ? index - 1 : index + 1; } else { indexOfMaxSibling = leftSibling != null ? index - 1 : index + 1; } } return indexOfMaxSibling; } // Gets the index of the specified value from the current node's values, // returning true if the value was found. Otherwise it returns false. private static bool TryGetIndexOf(BTreeNode<T> node, T value, out int valueIndex) { for (int index = 0; index < node.Values.Count; index++) { if (value.CompareTo(node.Values[index]) == 0) { valueIndex = index; return true; } } valueIndex = -1; return false; } // Finds the value of the predecessor value of a specific value in a node. // // Example: // // [3 6] // [1 2] [4 5] [7 8] // // The predecessor of 3 is 2. private static T FindPredecessor(BTreeNode<T> node, int index) { node = node.Children[index]; while (!node.Leaf) { node = node.Children.Last(); } return node.Values.Last(); } // Finds the value of the successor of a specific value in a node. // // Example: // // [3 6] // [1 2] [4 5] [7 8] // // The successor of 3 is 4. private static T FindSuccessor(BTreeNode<T> node, int index) { node = node.Children[index + 1]; while (!node.Leaf) { node = node.Children.First(); } return node.Values.First(); } |
Contains
Behavior | Returns true if the specified value exists in the tree. Otherwise it returns false. |
Performance | O(log n) |
public bool Contains(T value) { BTreeNode<T> node; int valueIndex; return TryFindNodeContainingValue(value, out node, out valueIndex); } // Searches the node and its children, looking for the specified value. internal bool TryFindNodeContainingValue(T value, out BTreeNode<T> node, out int valueIndex) { BTreeNode<T> current = root; // If the current node is null, then we never found the value. // Otherwise, we still have hope. while (current != null) { int index = 0; // Check each value in the node. while (index < current.Values.Count) { int compare = value.CompareTo(current.Values[index]); // Did we find it? if (compare == 0) { // Awesome! node = current; valueIndex = index; return true; } // If the value to find is less than the current node's value, // then we want to go left (which is where we are). if (compare < 0) { break; } // Otherwise, move on to the next value in the node. index++; } if (current.Leaf) { // If we are at a leaf node, there is no child to go // down to. break; } else { // Otherwise, go into the child we determined must contain the // value we want to find. current = current.Children[index]; } } node = null; valueIndex = -1; return false; } |
Clear
Behavior | Removes all values from the tree and sets the count to 0. |
Performance | O(1) |
public void Clear() { root = null; Count = 0; } |
Count
Behavior | Returns the number of values in the tree (0 if the tree is empty). |
Performance | O(1) |
public int Count { get; private set; } |
CopyTo
Behavior | Copies every value in the tree into the target array, starting at the specified index. |
Performance | O(n) |
public void CopyTo(T[] array, int arrayIndex) { foreach (T value in InOrderEnumerator(root)) { array[arrayIndex++] = value; } } |
IsReadOnly
Behavior | Returns a value indicating whether the tree is read-only. |
Performance | O(1) |
GetEnumerator
Behavior | Returns an enumerator that allows enumerating each of the values in the tree using an inorder (smallest to largest value) enumeration. |
Performance | O(1) to return the enumerator and O(n) to enumerate each item. |
public IEnumerator<T> GetEnumerator() { return InOrderEnumerator(root).GetEnumerator(); } System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() { return GetEnumerator(); } private IEnumerable<T> InOrderEnumerator(BTreeNode<T> node) { if (node != null) { if (node.Leaf) { foreach (T value in node.Values){ yield return value } } Else { IEnumerator<BTreeNode<T>> children = node.Children.GetEnumerator(); IEnumerator<T> values = node.Values.GetEnumerator(); while (children.MoveNext()) { foreach (T childValue in InOrderEnumerator(children.Current)) { yield return childValue; } if (values.MoveNext()) { yield return values.Current; } } } } } |
127 |

- 1800+ high-performance UI components.
- Includes popular controls such as Grid, Chart, Scheduler, and more.
- 24x5 unlimited support by developers.

