CHAPTER 4
AVL Tree
Balanced Tree Overview
An AVL tree is a self-balancing binary search tree. It is named after its inventors, G. M. Adelson-Velskii and E. M. Landis, who first described the structure and associated algorithms in 1962. Like the binary search tree introduced in the first book of this series, an AVL tree maintains these three simple rules:
- Each node in the tree will have at most two child nodes (the “left” and “right” children).
- Values smaller than the current node will go to the left.
- Values larger than or equal to the current node will go on the right.
In addition, the AVL tree adds a new rule:
- The height of the left and right nodes will never differ by more than 1.
What is Node Height?
The distance between any two related nodes can be measured.

Figure 30: Node Height
The previous figure shows a binary tree with lines indicating the levels of each set of nodes. The root node, 6, has no parent so it is at level 1. Nodes 4 and 8 are sibling nodes that are both at level 2. Nodes 3 and 5 are at level 3.
Using these levels we can easily find the distance between any two related nodes. For example, the distance between 6 and 5 is two (because node 6 is level 1 and node 5 is level 3; 3 minus 1 is equal to 2). Distance can be measured between non-root nodes as well. The distance between nodes 4 and 3 is one.
When talking about the height of a node’s children we are generally referring to the maximum height of the entire child tree.
For example, in Figure 30, the root node has a height of 2 because the maximum distance between the root (level 1) and the deepest leaf node (level 3) is 2.
With that understanding, let’s revisit the new rule: The height of the left and right nodes will never differ by more than 1.
What this means is that maximum height of the left child and right child will not differ by more than one and that rule will hold for every node in the tree. Seeing a few invalid balanced trees might help make this clearer.
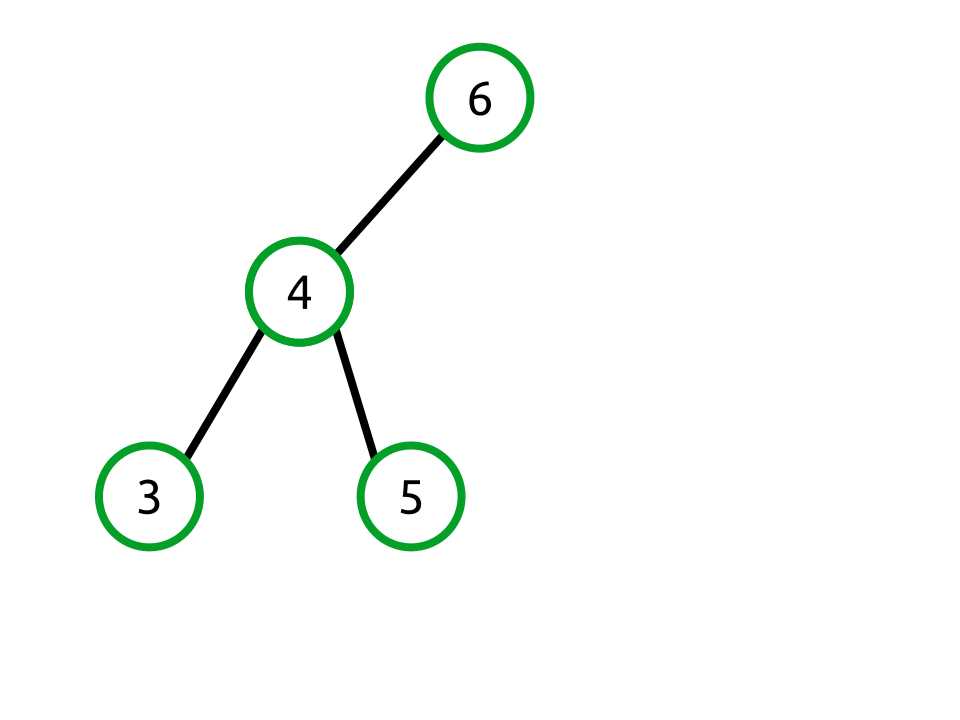
Figure 31: The root node has a left height of 2 and right height of 0.
This tree is not balanced because the right child of the root node has a height of two and the left child has a height of zero (because there is no left child).
Notice that node 4 is itself balanced because its left and right heights are both one.
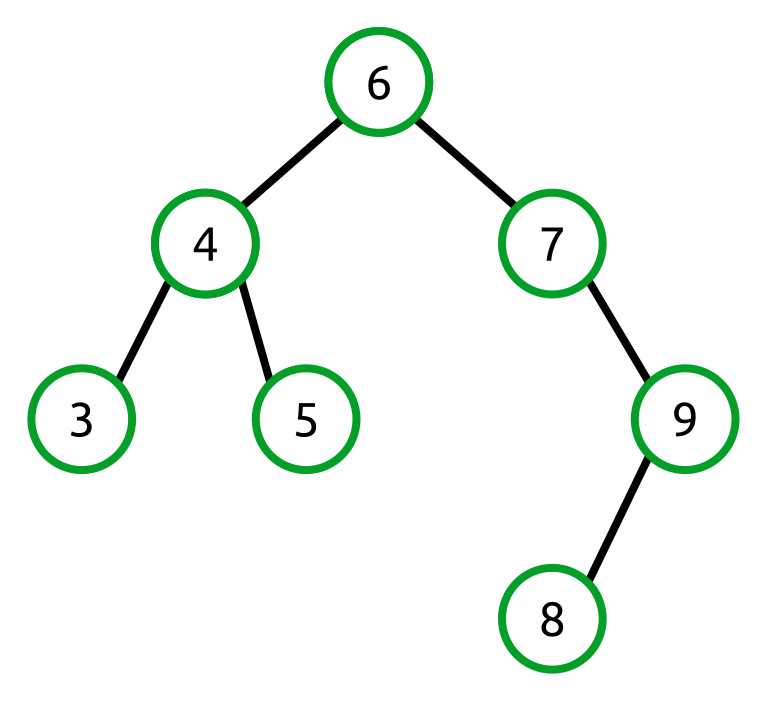
Figure 32: The root node is balanced but its right child is not
In this example, the left height of the root node is 2 and the right height is 3. While this may appear balanced, remember that the rule needs to apply recursively for every node in the tree. The node 7 is not balanced. It has a right height of 2 and a left height of 0.
Balancing Algorithms
With an understanding of what it means to be balanced, we now need to look at the mechanics of ensuring a tree is balanced. There are two steps to this. The first determines whether an operation leaves the tree in an unbalanced state. This is done by investigating the left and right child node heights during an operation that changes the structure of the tree (e.g., Add or Remove). The second balances the tree through a process known as node rotation.
AVL trees use two basic node rotations—left and right—and two composite rotations that use the basic rotations.
Right Rotation
Right rotation is the act of rotating nodes from left to right as shown in the following figure:

Figure 33: Right rotation moves the root’s left child into the root position

Figure 34: Right rotation moves the right child of the root’s left child to the left child of the old root
The algorithm for right rotation has three steps. These steps are all from the perspective of the original root node (B).
- Replace the current root with its immediate left child (this becomes the new root).
- The B node moves its left child (A) into its place.
- Move the new root’s right child to the old root’s left child.
- This changes B > C to D > C.
- Assign the old root (D) to be the new root’s (B) right child.
Left Rotation
Left rotation is the act of rotating a right-running series of nodes such that the middle of the series becomes the new root.
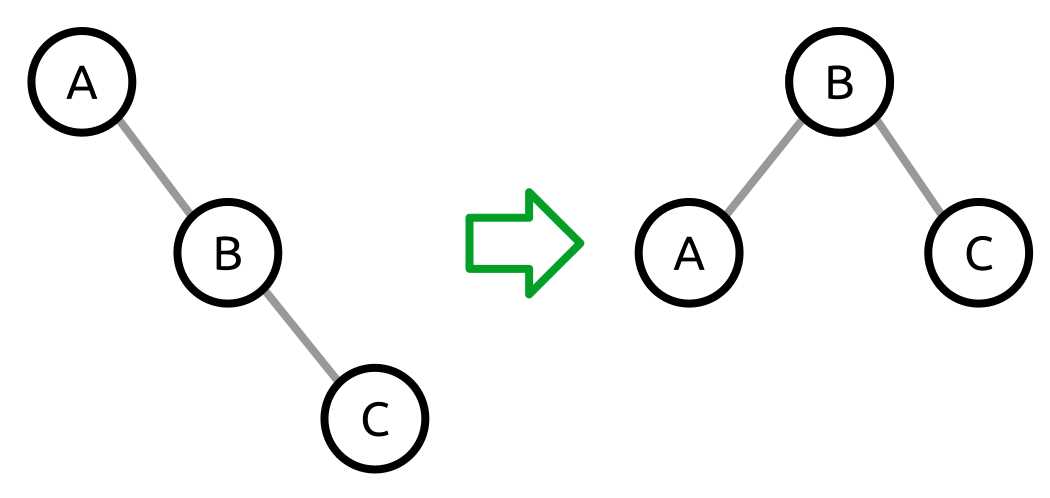
Figure 35: A left rotation moves the B node from the middle of the series to the root

Figure 36: A left rotation where the left child of the new root is moved to the right child of the old root
The algorithm for left rotation has three steps. These steps are all from the perspective of the original root node (A).
- Replace the current root with its immediate right child (the new root).
- This moves the A node's right child, C, into its place.
- Move the new root’s (C) left child, B, to the old root’s (A) right child.
- This changes C > B to A > B.
- Assign the old root (A) to be the new root’s (C) left child.
Right-Left Rotation
Right-left rotation applies a right rotation to the root node’s right child, followed by a left rotation at the root node. Why on Earth would we do this? Consider the following tree structure:
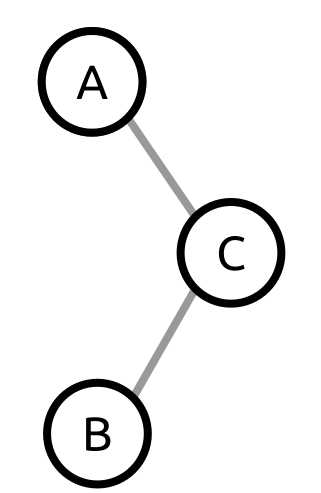
Figure 37: An unbalanced tree needing right-left rotation
Pay particular attention to the fact that this tree’s right child has a left child and not a right child. This is what distinguishes this situation from the example trees shown in the previous left and right rotation examples.
The tree is left heavy, so our gut reaction is to apply a right rotation. Using the right rotation algorithm described previously, we do the following:
- Move the C node into the root position.
- Move B from being C’s left child to A’s right child.
- Assign A as C’s left child.
Unfortunately, when we do that, the resulting tree is still unbalanced.

Figure 38: After applying the left rotation the tree is still unbalanced
At this point, the naïve solution would be to apply a right rotation which would bring us right back to where we started. Instead, we need to change the tree structure by first performing a right rotation of the right child.
Since we are performing a right rotation of the right child (C), we can ignore the root node (A) for a moment.

Figure 39: The right child subtree before and after the right rotation.
The right rotation moves the B node into the root position, moves C to its right child, and assigns the old root (C) to be the new right child of the new root (B).
In the context of the larger tree, our rotation transforms the tree like so:

Figure 40: A right rotation performed on the right child
The resulting tree (A > B > C) is something we know how to rotate using the left rotation algorithm. So the entire process looks like the following:

Figure 41: The entire right-left rotation process
Left-Right Rotation
Left-right rotation is simply the opposite of right-left rotation. We start with an unbalanced tree where the root node has a left child which has a right child but no left child. Once we have identified this situation, the solution is to apply a left rotation to the left child and then apply a right rotation to the root. The entire left-right rotation process is shown in the following figure:

Figure 42: The entire left-right rotation process
Heaviness and Balance Factor
Now that we know about the four rotation types, we need to know which one to pick when a tree is determined to be unbalanced. This is done through two measurements:
- Heaviness
- Balance factor
Heaviness is quite simply the difference between the left and right child node heights. If a tree has a larger left height, it is said to be “left heavy.” Conversely, if it has a larger right height, it is said to be “right heavy.”
Balance factor is the difference between the right and left heights. For example, if the right child node height of a tree is 5, and the left child node height is 3, the balance factor would be 2. Likewise, if the heights were reversed, the balance factor would be -2.

Figure 43: A right-heavy node (A). Its right child (C) has a balance factor of -1 because balance factor is the difference between the right height of C (0) and the left height (1).

Figure 44: A right-heavy node (A). Its right child (B) has a balance factor of 1 because the difference between its right child height (1) and left child height (0) is 1.
We will see how this all comes together in the Balance and Rotation Methods sections where the code for determining which rotation to run and the actual rotations is shown.
AVLTreeNode Class
The AVLTreeNode is a single node within the AVL tree. It provides properties to access the node’s left and right children, the node’s value, and a reference to the tree the node is contained in.
Additionally, it provides all of the methods necessary to determine the heights of the left and right children, its heaviness and balance factor, and provides the methods to perform the four rotation types.
public class AVLTreeNode<TNode> : IComparable<TNode> where TNode : IComparable { AVLTree<TNode> _tree; AVLTreeNode<TNode> _left; AVLTreeNode<TNode> _right; public AVLTreeNode(TNode value, AVLTreeNode<TNode> parent, AVLTree<TNode> tree) { Value = value; Parent = parent; _tree = tree; } public AVLTreeNode<TNode> Left { get { return _left; } internal set { _left = value; if (_left != null) { _left.Parent = this; } } } public AVLTreeNode<TNode> Right { get { return _right; } internal set { _right = value; if (_right != null) { _right.Parent = this; } } } public AVLTreeNode<TNode> Parent { get; internal set; } public TNode Value { get; private set; } /// <summary> /// Compares the current node to the provided value. /// </summary> /// <param name="other">The node value to compare to.</param> /// <returns>1 if the instance value is greater than the provided value, -1 if less, or 0 if equal.</returns> public int CompareTo(TNode other) { return Value.CompareTo(other); } // The rest of the code for the AVLTreeNode class is // in the subsequent sections of this chapter. } |
Balance
The balance algorithm determines if a rotation is needed, and if so, what rotation needs to be performed. It does this by first checking to see if the tree is unbalanced.
Being unbalanced is determined by checking if the tree is right or left heavy. A tree is right heavy if it has a right height more than 1 greater than the left height. Conversely, it is left heavy if it has a left height more than 1 greater than the right height.
If the tree is determined to be unbalanced, we need to next determine whether a simple right or left rotation will be sufficient, or if a right-left or left-right rotation will be needed.
This decision is made by looking at the left or right child of the root node, depending on whether it is right or left heavy. Next, the balance factor is looked at. These two comparisons are used to select the rotation algorithm.
Note: In this implementation, the heights of the trees are determined by walking the tree to find the longest path. This is conceptually simple, but not as efficient as it could be. As an exercise, consider other ways that the height of any node could be more efficiently determined.
internal void Balance() { if (State == TreeState.RightHeavy) { if (Right != null && Right.BalanceFactor < 0) { LeftRightRotation(); } else { LeftRotation(); } } else if (State == TreeState.LeftHeavy) { if (Left != null && Left.BalanceFactor > 0) { RightLeftRotation(); } else { RightRotation(); } } } private int MaxChildHeight(AVLTreeNode<TNode> node) { if (node != null) { return 1 + Math.Max(MaxChildHeight(node.Left), MaxChildHeight(node.Right)); } return 0; } private int LeftHeight { get { return MaxChildHeight(Left); } } private int RightHeight { get { return MaxChildHeight(Right); } } private TreeState State { get { if (LeftHeight - RightHeight > 1) { return TreeState.LeftHeavy; } if (RightHeight - LeftHeight > 1) { return TreeState.RightHeavy; } return TreeState.Balanced; } } private int BalanceFactor { get { return RightHeight - LeftHeight; } } enum TreeState { Balanced, LeftHeavy, RightHeavy, } |
Rotation Methods
The rotations are implementations of the algorithms discussed in the Balancing Algorithms section. The ReplaceRoot method handles the mechanics of moving the child node into the root node’s position. The parent node of the original root needs to be updated to point to the new root node. If there is no parent node, the containing tree needs to be made aware of the new tree root node.
private void LeftRotation() { // a // \ // b // \ // c // // becomes // b // / \ // a c AVLTreeNode<TNode> newRoot = Right; // Replace the current root with the new root. ReplaceRoot(newRoot); // Take ownership of right's left child as right (now parent). Right = newRoot.Left; // The new root takes this as its left. newRoot.Left = this; } private void RightRotation() { // c (this) // / // b // / // a // // becomes // b // / \ // a c AVLTreeNode<TNode> newRoot = Left; // Replace the current root with the new root. ReplaceRoot(newRoot); // Take ownership of left's right child as left (now parent). Left = newRoot.Right; // The new root takes this as its right. newRoot.Right = this; } private void LeftRightRotation() { Right.RightRotation(); LeftRotation(); } private void RightLeftRotation() { Left.LeftRotation(); RightRotation(); } private void ReplaceRoot(AVLTreeNode<TNode> newRoot) { if (this.Parent != null) { if (this.Parent.Left == this) { this.Parent.Left = newRoot; } else if (this.Parent.Right == this) { this.Parent.Right = newRoot; } } else { _tree.Head = newRoot; } newRoot.Parent = this.Parent; this.Parent = newRoot; } |
AVLTree Class
The AVL tree class provides the basic collection methods to add, remove, enumerate, and check if a value exists within the tree. Additionally, it provides the ability to clear the tree and get the count of nodes in the tree.
public class AVLTree<T> : IEnumerable<T> where T : IComparable { public AVLTreeNode<T> Head { get; internal set; } public void Add(T value); public bool Contains(T value); public bool Remove(T value); public IEnumerator<T> GetEnumerator(); System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator(); public void Clear(); public int Count { get; private set; } } |
Add
Behavior | Adds the specific value to the tree, ensuring that the tree is in a balanced state when the method completes. |
Performance | O(log n) |
The AVL tree Add operation is nearly identical to the binary search tree add operation. It walks the tree using the rules described previously in this chapter. Once the appropriate node location is found, the node is inserted into the tree. Since the tree might now be unbalanced, the node performs the balance operation to ensure the tree is balanced when the Add method returns.
public void Add(T value) { // Case 1: The tree is empty--allocate the head. if (Head == null) { Head = new AVLTreeNode<T>(value, null, this); } // Case 2: The tree is not empty--find the right location to insert. else { AddTo(Head, value); } Count++; } // Recursive add algorithm. private void AddTo(AVLTreeNode<T> node, T value) { // Case 1: Value is less than the current node value. if (value.CompareTo(node.Value) < 0) { // If there is no left child, make this the new left. if (node.Left == null) { node.Left = new AVLTreeNode<T>(value, node, this); } else { // Else, add it to the left node. AddTo(node.Left, value); } } // Case 2: Value is equal to or greater than the current value. else { // If there is no right, add it to the right. if (node.Right == null) { node.Right = new AVLTreeNode<T>(value, node, this); } else { // Else, add it to the right node. AddTo(node.Right, value); } } node.Balance(); } |
Contains
Behavior | Returns true if the specific value is contained within the tree. Otherwise it returns false. |
Performance | O(log n) |
A traditional binary search tree has O(n) worst-case complexity because a pathologically unbalanced tree is basically a linked list. Because an AVL tree is balanced, we have a guaranteed complexity of O(log n).
public bool Contains(T value) { return Find(value) != null; } /// <summary> /// Finds and returns the first node containing the specified value. If the value /// is not found, it returns null. It also returns the parent of the found node (or null) /// which is used in Remove. /// </summary> /// <param name="value">The value to search for.</param> /// <param name="parent">The parent of the found node (or null).</param> /// <returns>The found node (or null).</returns> private AVLTreeNode<T> Find(T value) { // Now, try to find data in the tree. AVLTreeNode<T> current = Head; // While we don't have a match... while (current != null) { int result = current.CompareTo(value); if (result > 0) { // If the value is less than current, go left. current = current.Left; } else if (result < 0) { // If the value is greater than current, go right. current = current.Right; } else { // We have a match! break; } } return current; } |
Remove
Behavior | If the specified value exists within the tree, the value is removed and the method returns true. Otherwise the method returns false. |
Performance | O(log n) |
Like Add, the Remove method works just like the traditional binary search tree Remove algorithm; however, it adds a balance operation performed on the parent of the deleted node.
The binary search tree delete algorithm is somewhat complex and described in detail in Data Structures Succinctly Part 1.
/// <summary> /// Removes the first occurrence of the specified value from the tree. /// </summary> /// <param name="value">The value to remove.</param> /// <returns>True if the value was removed; false otherwise.</returns> public bool Remove(T value) { AVLTreeNode<T> current; current = Find(value); if (current == null) { return false; } AVLTreeNode<T> treeToBalance = current.Parent; Count--; // Case 1: If current has no right child, then current's left replaces current. if (current.Right == null) { if (current.Parent == null) { Head = current.Left; if (Head != null) { Head.Parent = null; } } else { int result = current.Parent.CompareTo(current.Value); if (result > 0) { // If the parent value is greater than the current value, // make the current left child a left child of parent. current.Parent.Left = current.Left; } else if (result < 0) { // If the parent value is less than the current value, // make the current left child a right child of parent. current.Parent.Right = current.Left; } } } // Case 2: If current's right child has no left child, then current's right child // replaces current. else if (current.Right.Left == null) { current.Right.Left = current.Left; if (current.Parent == null) { Head = current.Right; if (Head != null) { Head.Parent = null; } } else { int result = current.Parent.CompareTo(current.Value); if (result > 0) { // If the parent value is greater than the current value, // make the current right child a left child of parent. current.Parent.Left = current.Right; } else if (result < 0) { // If the parent value is less than the current value, // make the current right child a right child of parent. current.Parent.Right = current.Right; } } } // Case 3: If current's right child has a left child, replace current with current's // right child's leftmost child. else { // Find the right's leftmost child. AVLTreeNode<T> leftmost = current.Right.Left; while (leftmost.Left != null) { leftmost = leftmost.Left; } // The parent's left subtree becomes the leftmost's right subtree. leftmost.Parent.Left = leftmost.Right; // Assign leftmost's left and right to current's left and right children. leftmost.Left = current.Left; leftmost.Right = current.Right; if (current.Parent == null) { Head = leftmost; if (Head != null) { Head.Parent = null; } } else { int result = current.Parent.CompareTo(current.Value); if (result > 0) { // If the parent value is greater than the current value, // make leftmost the parent's left child. current.Parent.Left = leftmost; } else if (result < 0) { // If the parent value is less than the current value, // make leftmost the parent's right child. current.Parent.Right = leftmost; } } } if (treeToBalance != null) { treeToBalance.Balance(); } else { if (Head != null) { Head.Balance(); } } return true; } |
GetEnumerator
Behavior | Returns an enumerator that performs an inorder traversal of the AVL tree. |
Performance | O(1) to return the enumerator. O(n) for the caller to enumerate each node. |
The inorder (smallest to largest value) traversal algorithm is described in more detail in book one of this series. The implementation that follows uses a stack to demonstrate performing the traversal without recursion.
/// <summary> /// Enumerates the values contained in the binary tree in inorder traversal order. /// </summary> /// <returns>The enumerator.</returns> public IEnumerator<T> InOrderTraversal() { // This is a non-recursive algorithm using a stack to demonstrate removing // recursion to make using the yield syntax easier. if (Head != null) { // Store the nodes we've skipped in this stack (avoids recursion). Stack<AVLTreeNode<T>> stack = new Stack<AVLTreeNode<T>>(); AVLTreeNode<T> current = Head; // When removing recursion, we need to keep track of whether // we should be going to the left nodes or the right nodes next. bool goLeftNext = true; // Start by pushing Head onto the stack. stack.Push(current); while (stack.Count > 0) { // If we're heading left... if (goLeftNext) { // Push everything but the leftmost node to the stack. // We'll yield the leftmost after this block. while (current.Left != null) { stack.Push(current); current = current.Left; } } // Inorder is left -> yield -> right yield return current.Value; // If we can go right, then do so. if (current.Right != null) { current = current.Right; // Once we've gone right once, we need to start // going left again. goLeftNext = true; } else { // If we can't go right we need to pop off the parent node // so we can process it and then go to its right node. current = stack.Pop(); goLeftNext = false; } } } } /// <summary> /// Returns an enumerator that performs an inorder traversal of the binary tree. /// </summary> /// <returns>The inorder enumerator.</returns> public IEnumerator<T> GetEnumerator() { return InOrderTraversal(); } /// <summary> /// Returns an enumerator that performs an inorder traversal of the binary tree. /// </summary> /// <returns>The inorder enumerator.</returns> System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() { return GetEnumerator(); } |
Clear
Behavior | Removes all the nodes from the tree. |
Performance | O(1) |
public void Clear() { Head = null; Count = 0; } |
Count
Behavior | Returns the number of nodes currently contained in the tree. |
Performance | O(1) |
public int Count { get; private set; } |

- 1800+ high-performance UI components.
- Includes popular controls such as Grid, Chart, Scheduler, and more.
- 24x5 unlimited support by developers.

