Skip Lists

Overview

In the previous book, we looked at two common list-like data structures: the linked list and the array list. Each data structure came with a set of trade-offs. Now I’d like to add a third into the mix: the skip list.

A skip list is an ordered (sorted) list of items stored in a linked-list structure in a way that allows O(log n) insertion, removal, and search. So it looks like an ordered list, but has the operational complexity of a balanced tree.

Why is this compelling? Doesn’t a sorted array give you O(log n) search as well? Sure, but a sorted array doesn’t give you O(log n) insertion or removal. Okay, why not just use a tree? Well, you could. But as we will see, the implementation of the skip list is much less complex than an unbalanced tree, and far less complex than a balanced one. Also, at the end of the chapter I’ll examine at another benefit of a skip list that wouldn’t be too hard to add—array-style indexing.

So if a skip list is as good as a balanced tree while being easier to implement, why don’t more people use them? I suspect it is a lack of awareness. Skip lists are a relatively new data structure—they were first documented by William Pugh in 1990—and as such are not a core part of most algorithm and data structure courses.

How It Works

Let’s start by looking at an ordered linked list in memory.

Figure 1: A sorted linked list represented in memory

I think we can all agree that searching for the value 8 would require an O(n) search that started at the first node and went to the last node.

So how can we cut that in half? Well, what if we were able to skip every other node? Obviously, we can’t get rid of the basic Next pointer—the ability to enumerate each item is critical. But what if we had another set of pointers that skipped every other node? Now our list might look like this:

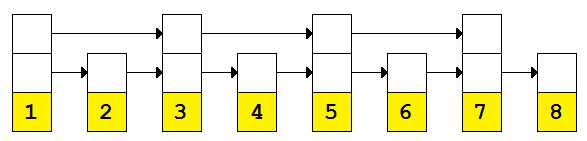
Figure 2: Sorted linked list with pointers skipping every other node

Our search would be able to perform one half the comparisons by using the wider links. The orange path shown in the following figure demonstrates the search path. The orange dots represent points where comparisons were performed—it is comparisons we are measuring when determining the complexity of the search algorithm.

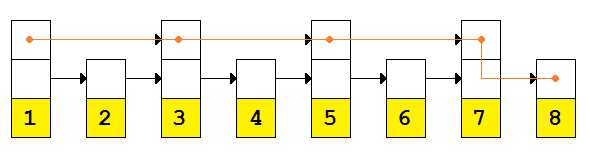
Figure 3: Search path across new pointers

O(n) is now roughly O(n/2). That’s a decent improvement, but what would happen if we added another layer?

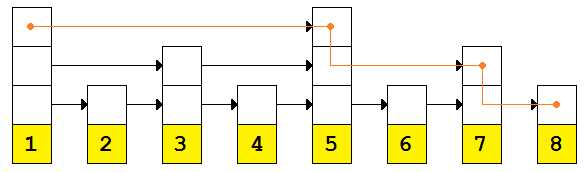
Figure 4: Adding an additional layer of links

We’re now down to four comparisons. If the list were nine items long, we could find the value 9 in using only O(n/3) comparisons.

With each additional layer of links, we can skip more and more nodes. This layer skipped three. The next would skip seven. The one after that skips 15 at a time.

Going back to Figure 4, let’s look at the specific algorithm that was used.

We started at the highest link on the first node. Since that node’s value (1) did not match the value we sought (8), we checked the value the link pointed to (5). Since 5 was less than the value we wanted, we went to that node and repeated the process.

The 5 node had no additional links at the third level, so we went down to level two. Level two had a link so we compared what it pointed to (7) against our sought value (8). Since the value 7 was less than 8, we followed that link and repeated.

The 7 node had no additional links at the second level so we went down to the first level and compared the value the link pointed to (8) with the value we sought (8). We found our match.

While the mechanics are new, this method of searching should be familiar. It is a divide and conquer algorithm. Each time we followed a link we were essentially cutting the search space in half.

But There Is a Problem

There is a problem with the approach we took in the previous example. The example used a deterministic approach to setting the link level height. In a static list this might be acceptable, but as nodes are added and removed, we can quickly create pathologically bad lists that become degenerate linked lists with O(n) performance.

Let’s take our three-level skip list and remove the node with the value 5 from the list.

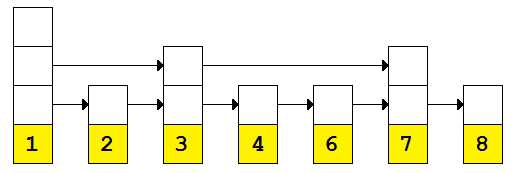
Figure 5: Skip list with 5 node removed

With 5 gone, our ability to traverse the third-level links is gone, but we’re still able to find the value 8 in four comparisons (basically O(n/2)). Now let’s remove 7.

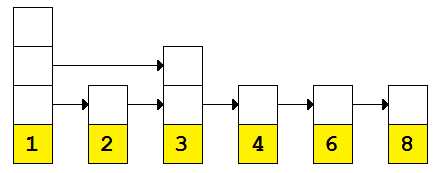
Figure 6: Skip list with 5 and 7 nodes removed

We can now only use a single level-two link and our algorithm is quickly approaching O(n). Once we remove the node with the value 3, we will be there.

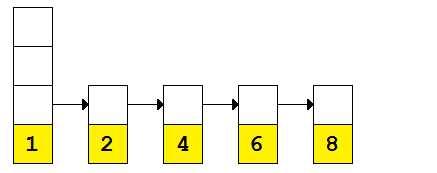
Figure 7: Skip list with 3, 5, and 7 nodes removed

And there we have it. With a series of three carefully planned deletions, the search algorithm went from being O(n/3) to O(n).

To be clear, the problem is not that this situation can happen, but rather that the situation could be intentionally created by an attacker. If a caller has knowledge about the patterns used to create the skip list structure, then he or she could craft a series of operations that create a scenario like what was just described.

The easiest way to mitigate this, but not entirely prevent it, is to use a randomized height approach. Basically, we want to create a strategy that says that 100% of nodes have the first-level link (this is mandatory since we need to be able to enumerate every node in order), 50% of the nodes have the second level, 25% have the third level, etc. Because a random approach is, well, random, it won’t be true that exactly 50% or 25% have the second or third levels, but over time, and as the list grows, this will become true.

Using a randomized approach, our list might look something like this:

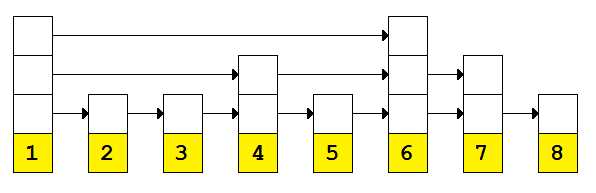
Figure 8: Skip list with randomized height

The lack of a pattern that can be manipulated means that the probability of our algorithm being O(log n) increases as the number of items in the list increases.

Code Samples

The code samples found in this book can be downloaded at https://bitbucket.org/syncfusion/data_structures_succinctly_part2.

SkipListNode Class

Like the linked list we saw in the first book, the skip list has a node class to contain the value as well as the item’s collection of links. The Next collection is an array of links to subsequent nodes (or null if no link is present).

SkipList Class

The SkipList<T> class is a generic class that implements the ICollection<T> interface and requires the generic type argument, T, be of a type that implements the IComparable<T> interface. Since skip lists are an ordered collection, it is a requirement that the contained type implements the IComparable<T> interface.

There are a few private fields in addition to the ICollection<T> method and properties. The _rand field provides access to a random number generator that will be used to randomly determine the node link height. The _head field is a node which does not contain any data, but has a maximum link height—this is important because it will serve as a starting point for all traversals. The _levels field is the current maximum link height in use by any node (not including the _head node). _count is the number of items contained in the list.

The remaining methods and properties are required to implement the ICollection<T> interface:

Add

The add algorithm for skip lists is fairly simple:

1. Pick a random height for the node (PickRandomLevel method).
2. Allocate a node with the random height and a specific value.
3. Find the appropriate place to insert the node into the sorted list.
4. Insert the node.

Picking a Level

As stated previously, the random height needs to be scaled logarithmically. 100% of the values must be at least 1—a height of 1 is the minimum needed for a regular linked list. 50% of the heights should be 2. 25% should be level 3, and so on.

Any algorithm that satisfies this scaling is suitable. The algorithm demonstrated here uses a random 32-bit value and the generated bit pattern to determine the height. The index of the first LSB bit that is a 1, rather than a 0, is the height that will be used.

Let’s look at the process by reducing the set from 32 bits to 4 bits, and looking at the 16 possible values and the height from that value.

With these 16 values, you can see the distribution works as we expect. 100% of the heights are at least 1. 50% are at least height 2.

Taking this further, the following chart shows the results of calling PickRandomLevel one million times. You can see that all one million are at least 1 in height, and the scaling from there falls off exactly as we expect.

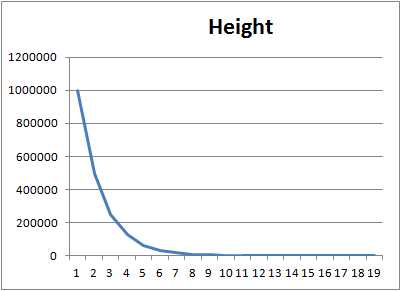
Figure 9: Minimum height values picked one million times

Picking the Insertion Point

The insertion point is found using the same algorithm described for the Contains method. The primary difference is that at the point where Contains would return true or false, the following is true:

1. The current node is less than or equal to the value being inserted.
2. The next node is greater than or equal to the value being inserted.

This is a valid point to insert the new node.

Remove

The Remove operation determines if the node being searched for exists in the list and, if so, removes it from the list using the normal linked list item removal algorithm.

The search algorithm used is the same method described for the Contains method.

Contains

The Contains operation starts at the tallest link on the first node and checks the value at the end of the link. If that value is less than or equal to the sought value, the link can be followed; but if the linked value is greater than the sought value, we need to drop down one height level and try the next link there. Eventually, we will either find the value we seek or we will find that the node does not exist in the list.

The following image demonstrates how the number 5 is searched for within the skip list.

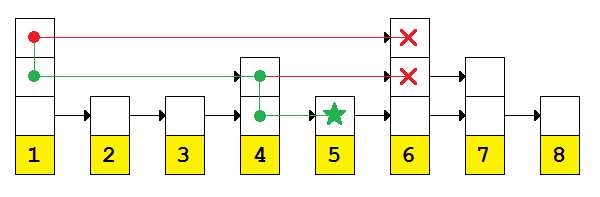
Figure 10: Searching a skip list for the value 5

The first comparison is performed at the topmost link. The linked value, 6, is greater than the value being sought (5), so instead of following the link the search repeats at the next lower height.

The next lower link is connected to a node with the value 4. This is less than the value being sought, so the link is followed.

The 4 node at height 2 is linked to the node with the value 6. Since this is greater than the value we're looking for, the link cannot be followed and the search cycle repeats at the next lower level.

At this point, the link points to the node containing the value 5, which is the value we sought.

Clear

Clear reinitializes the head of the list and sets the current count to 0.

CopyTo

The CopyTo method uses the class enumerator to enumerate the items in the list and copies each item into the target array.

IsReadOnly

In this implementation, the skip list is hardcoded not to be read-only.

Count

GetEnumerator

The enumeration method simply walks the list at height 1 (array index 0). This is the list whose links are always to the next node in the list.

Common Variations

Array-Style Indexing

A common change made to the skip list is to provide index-based item access; for example, the n-th item could be accessed by the caller using array-indexing syntax.

This could easily be implemented in O(n) time by simply walking the first level links, but an optimized approach would be to track the length of each link and use that information to walk to the appropriate link. An example list might be visualized like this:

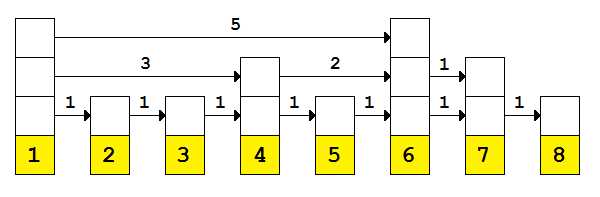
Figure 11: A skip list with link lengths

With these lengths we can implement array-like indexing in O(log n) time—it uses the same algorithm as the Contains method, but instead of checking the value on the end of the link we simply check the link length.

Making this change is not terribly difficult, but it is a little more complex than simply adding the length attribute. The Add and Remove methods need to be updated to set the length of all affected links, at all heights, after each operation.

Set behaviors

Another common change is to implement a Set (or Set-like behaviors) by not allowing duplicate values in the list. Because this is a relatively common usage of skip lists, it is important to understand how your list handles duplicates before using it.